Решение.
Траектории СП X(t) имеют вид 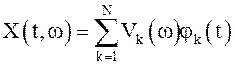 , где
, где ![]() - неслучайные числа, следовательно, для
всех
- неслучайные числа, следовательно, для
всех 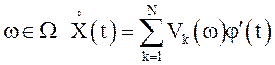 . Если X(t)- с.к. дифференцируемый СП, то
его производная согласно вышеизложенному совпадает почти всюду с производной
траекторий
. Если X(t)- с.к. дифференцируемый СП, то
его производная согласно вышеизложенному совпадает почти всюду с производной
траекторий ![]() , то есть
, то есть 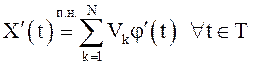 .
.
Остается проверить с.к. дифференцируемость СП X(t) по
теореме 4: 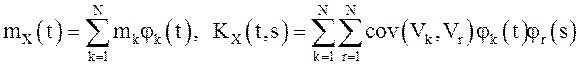 - дифференцируемы нужное число раз, при
этом
- дифференцируемы нужное число раз, при
этом 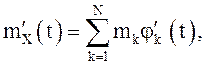
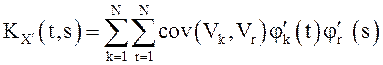 .
.
Определение интеграла от случайной функции X(t), ![]() , дословно повторяет определение интеграла
Римана на отрезке
, дословно повторяет определение интеграла
Римана на отрезке ![]() . Пусть X(t) –
случайная с.к. непрерывная функция,
. Пусть X(t) –
случайная с.к. непрерывная функция, ![]() - неслучайная
непрерывная функция двух переменных
- неслучайная
непрерывная функция двух переменных ![]() ,
, ![]() - некоторое разбиение отрезка
- некоторое разбиение отрезка ![]() с мелкостью разбиения
с мелкостью разбиения ![]() . Выберем на отрезках
. Выберем на отрезках ![]() длины
длины ![]() произвольные
(не случайные!) точки
произвольные
(не случайные!) точки ![]() и составим сумму
и составим сумму 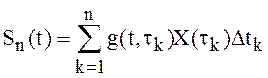 .
.
Определение 6. С.к.
интегралом от СФ ![]() по области Т называется с.к.
предел последовательности интегральных сумм
по области Т называется с.к.
предел последовательности интегральных сумм ![]() при
при ![]() , если он существует:
, если он существует: 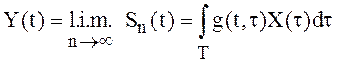 .
.
Интеграл 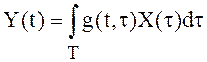 называют еще с.к.
интегралом от СФ X(t) с весом
называют еще с.к.
интегралом от СФ X(t) с весом ![]() .
.
Теорема 5.
С.к. интеграл от СФ X(t) с весом ![]() по промежутку
по промежутку ![]() существует тогда и только тогда, когда
существует интеграл
существует тогда и только тогда, когда
существует интеграл
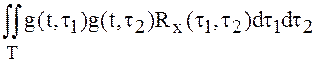 , или, что то же самое, с.к.
интеграл от СФ Х(t) с весом
, или, что то же самое, с.к.
интеграл от СФ Х(t) с весом ![]() по промежутку
по промежутку ![]() существует тогда и только тогда, когда
существуют интегралы
существует тогда и только тогда, когда
существуют интегралы 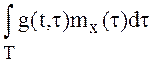 и
и 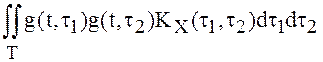 .
.
Доказательство теорем опирается на стохастический критерий Коши с.к. сходимости. Справедливы соотношения:
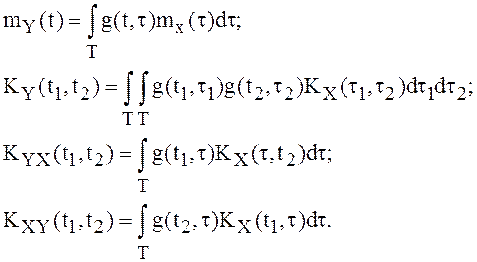 (3)
(3)
При этом 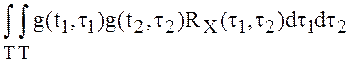 представляет собой
момент второго порядка для интеграла Y(t), то есть
представляет собой
момент второго порядка для интеграла Y(t), то есть 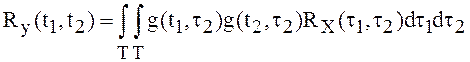 .
.
В частном случае, когда ![]() зависит
только от
зависит
только от ![]() , то есть
, то есть ![]() , с.к.
интеграл от СФ X(t) с весом
, с.к.
интеграл от СФ X(t) с весом ![]() будет уже просто
случайной величиной
будет уже просто
случайной величиной 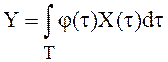 , для которой первые две формулы
из (3) принимают вид:
, для которой первые две формулы
из (3) принимают вид: 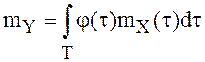 ,
, 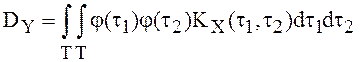 .
.
Формулы (3) легко можно доказать, опираясь на определение ковариационной матрицы и замечание в конце п.3.1.
Если X(t) – n-мерный СП, тогда ![]() -
матрица размерности
-
матрица размерности ![]() и все формулы (3) имеют место с
очевидными изменениями: вторая из них запишется в виде:
и все формулы (3) имеют место с
очевидными изменениями: вторая из них запишется в виде:
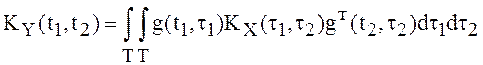 , а
последняя - в виде:
, а
последняя - в виде:
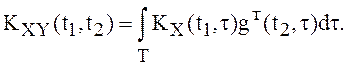
Среднеквадратический интеграл Y(t) обладает некоторыми свойствами определенного интеграла:
1. Если ![]() - с.к.
непрерывная на Т функция, то с.к. интеграл Y(t) существует.
- с.к.
непрерывная на Т функция, то с.к. интеграл Y(t) существует.
2.Линейность
интеграла: 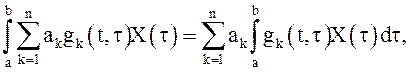 где
где ![]() неслучайные
коэффициенты, а
неслучайные
коэффициенты, а ![]() - с.к. интегрируемые на отрезке
функции.
- с.к. интегрируемые на отрезке
функции.
3. Правило дифференцирования по верхнему пределу.
Прежде всего введем определение такого интеграла.
Если 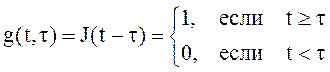 ,
, 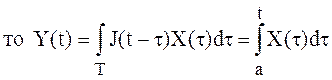 - интеграл с переменным верхним пределом
интегрирования. В более общем виде такие интегралы имеют вид
- интеграл с переменным верхним пределом
интегрирования. В более общем виде такие интегралы имеют вид
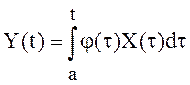 ,
(4) где
,
(4) где
![]() , X – с.к. непрерывная cлучайная
функция.
, X – с.к. непрерывная cлучайная
функция.
Для интеграла 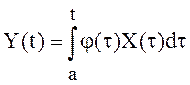 существует
производная
существует
производная
![]() (5)
(5)
Этот результат можно получить, если рассмотреть 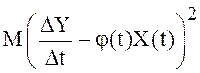 и показать, что в пределе при
и показать, что в пределе при ![]() это выражение обращается в нуль.
это выражение обращается в нуль.
В рассматриваемом случае из равенств
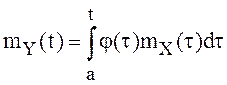 ,
, 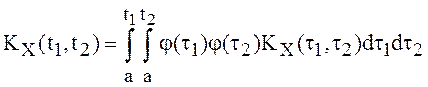
в точках непрерывности подынтегральных функций следуют равенства
![]() ,
, 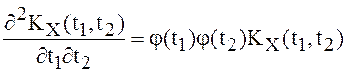 .
.
4.
Интегрирование по частям. Если в интеграле Y(t) ![]() , Х(t)
– с.к. непрерывная случайная функция , имеющая с.к. производную
, Х(t)
– с.к. непрерывная случайная функция , имеющая с.к. производную ![]() , тогда справедлива формула
, тогда справедлива формула
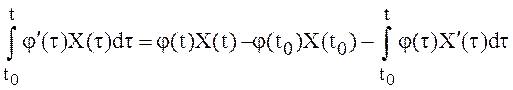 (6)
(6)
Из формулы (6), рассматривая интеграл в левой части
как с.к. предел интегральных сумм и учитывая непрерывность дифференцируемой
функции ![]() , можно получить формулу для с.к.
производной произведения:
, можно получить формулу для с.к.
производной произведения:
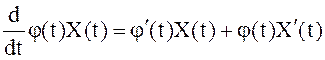 .
.
Пример 7. Пусть
W(t), ![]() , стандартный
винеровский процесс. Докажем, что он с.к. интегрируем на Т с весом
, стандартный
винеровский процесс. Докажем, что он с.к. интегрируем на Т с весом ![]() .
.
Решение. Воспользуемся
теоремой 5. Среднеквадратический интеграл 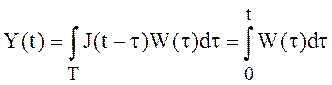 существует,
если существует интеграл
существует,
если существует интеграл 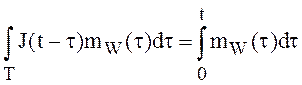 и существует интеграл
и существует интеграл
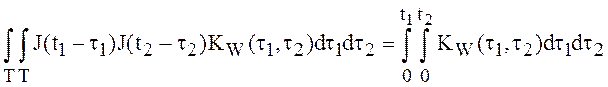 .
.
Знаем,
что ![]() ,
, ![]() . Но
тогда
. Но
тогда
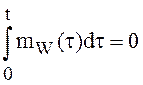 и
и 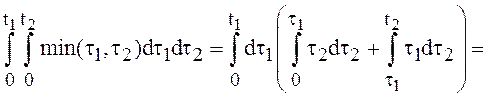
=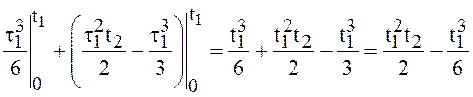 .
.
Оба интеграла конечны, следовательно, существует и интеграл Y(t).
Пример 8. Найти
![]() , если
, если
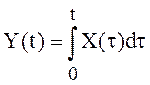 ,
, ![]() .
.
Решение.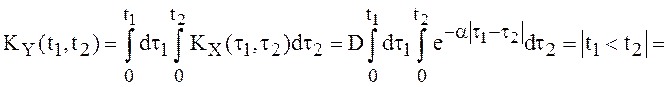
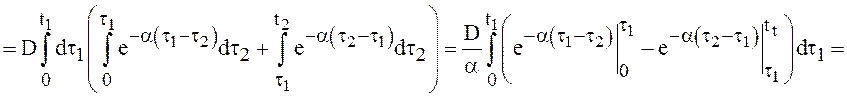
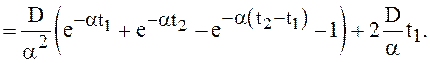
При ![]() вследствие симметрии
матрицы
вследствие симметрии
матрицы ![]() выражение для
выражение для ![]() будет
аналогичным, только
будет
аналогичным, только ![]() и
и ![]() поменяются
местами. Окончательно получаем
поменяются
местами. Окончательно получаем
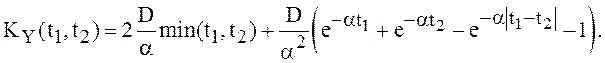
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.