Все операции математического анализа опираются на понятия предела и сходимости.
Если же определять операции анализа над случайными функциями, неизбежно приходится опираться на понятие вероятностной сходимости. Но вероятностной сходимости существует много видов, какую из них предпочесть? В теории вероятностей мы рассматривали сходимость по вероятности, с вероятностью 1 (почти наверное), в среднем квадратическом, по распределению.
В теории случайных процессов предпочтение отдается средней квадратичной сходимости или с.к. сходимости, поскольку при этом виде сходимости получается довольно несложная теория дифференцирования и интегрирования случайных функций, дающая удобные практические методы исследования случайных функций.
Для последовательностей случайных величин ![]() среднюю квадратическую сходимость мы
рассматривали в теории вероятностей. Определение с.к. сходимости аналогично в
случае однопараметрического семейства случайных величин
среднюю квадратическую сходимость мы
рассматривали в теории вероятностей. Определение с.к. сходимости аналогично в
случае однопараметрического семейства случайных величин ![]() с
конечными моментами второго порядка: говорят, что
с
конечными моментами второго порядка: говорят, что ![]() с.к.
сходится к X при
с.к.
сходится к X при ![]() ,
, 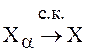 , если
, если ![]()
![]() .
.
Лемма Лоэва.
Пусть ![]() ,
, ![]() - два
семейства случайных величин и
- два
семейства случайных величин и 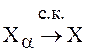 ,
, ![]() ,
, 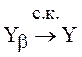 ,
, ![]() . Тогда
. Тогда ![]() ,
, ![]() .
.
Доказательство.
![]() . Применим к каждому слагаемому правой
части известное из теории вероятностей неравенство для моментов второго порядка
(неравенство Шварца):
. Применим к каждому слагаемому правой
части известное из теории вероятностей неравенство для моментов второго порядка
(неравенство Шварца):
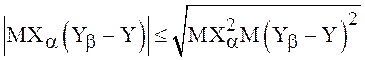 ,
, 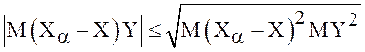 , далее,
учитывая, что
, далее,
учитывая, что ![]() остается ограниченной величиной
при
остается ограниченной величиной
при ![]() , так как
, так как
![]()
![]() , получим результат.
, получим результат.
Следствие 1. Если
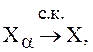
![]() , то
, то ![]() ,
, ![]() .
.
Следствие 2. Если
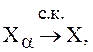
![]() , то
для любой с. в. Y
, то
для любой с. в. Y ![]() ,
,![]() .
.
Следствие 3.
Если 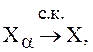
![]() , то
, то
![]() ,
, 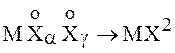 ,
, ![]() .
.
Для доказательства последнего результата достаточно
воспользоваться равенством 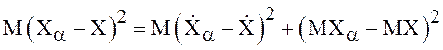 , на основании которого
можно утверждать, что с.к. сходимость
, на основании которого
можно утверждать, что с.к. сходимость ![]()
![]() ,
влечет сходимость
,
влечет сходимость ![]() ,
,![]() , и с.к. сходимость
, и с.к. сходимость ![]()
![]() . Затем к последнему из полученных
результатов следует применить следствие 1.
. Затем к последнему из полученных
результатов следует применить следствие 1.
Можно доказать обратное по отношению к лемме Лоэва
утверждение: если существует 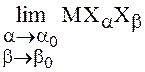 , то существует и с.к.
предел с. в.
, то существует и с.к.
предел с. в. ![]() при
при ![]() .
.
Действительно, пусть 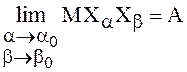 .
Рассмотрим
.
Рассмотрим
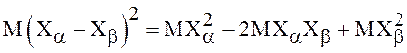 . Перейдем к пределу при
. Перейдем к пределу при ![]() ,
, ![]() :
: 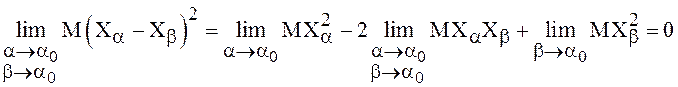 , так
как предел каждого из слагаемых правой части равен А. Следовательно,
, так
как предел каждого из слагаемых правой части равен А. Следовательно, ![]() - фундаментальна и, значит, существует
с.к. предел для
- фундаментальна и, значит, существует
с.к. предел для ![]() .
.
Теперь можно сформировать так называемый стохастический критерий Коши с.к. сходимости:
Для
с.к. сходимости с.в. ![]() к некоторой с.в. X при
к некоторой с.в. X при ![]() необходимо и достаточно сходимости
необходимо и достаточно сходимости ![]() к неотрицательному пределу при
к неотрицательному пределу при ![]() .
.
Или, что то же самое, для с.к. сходимости с.в. ![]() к
некоторой с.в. X при
к
некоторой с.в. X при ![]() необходимо и достаточно
сходимости 1)
необходимо и достаточно
сходимости 1) ![]() к конечному пределу при
к конечному пределу при ![]() и 2) центрального момента
и 2) центрального момента ![]() к конечному пределу при
к конечному пределу при ![]() .
.
Замечание.
Если 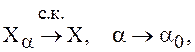 то есть
то есть 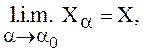 тогда
тогда
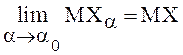 (следствие 3 леммы Лоэва). Последнее
равенство с учетом первого соотношения перепишем в виде
(следствие 3 леммы Лоэва). Последнее
равенство с учетом первого соотношения перепишем в виде
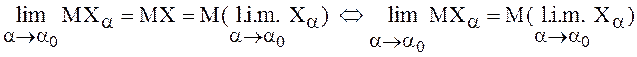 .
.
Пример 1. Пусть
X(t), ![]() , - винеровский
скалярный процесс с единичным коэффициентом диффузии. Пусть
, - винеровский
скалярный процесс с единичным коэффициентом диффузии. Пусть ![]() и
и ![]() , и
, и ![]() . Покажем, что существует с.к. предел
. Покажем, что существует с.к. предел
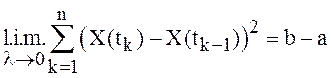 .
.
Решение. Согласно
определению винеровского процесса случайные величины ![]() ,
,
![]() , независимы, имеют нулевое математическое
ожидание и дисперсии
, независимы, имеют нулевое математическое
ожидание и дисперсии 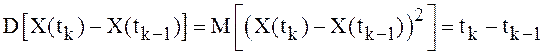 .
.
Так как
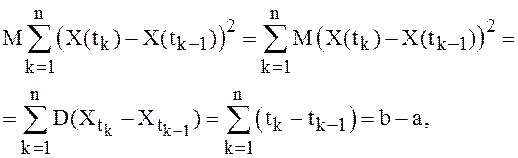
то
очевидно, что 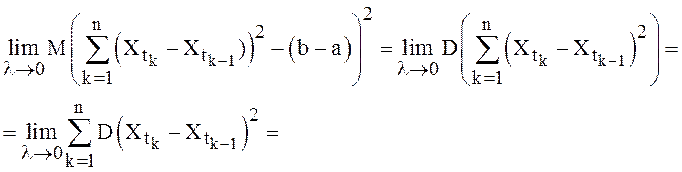
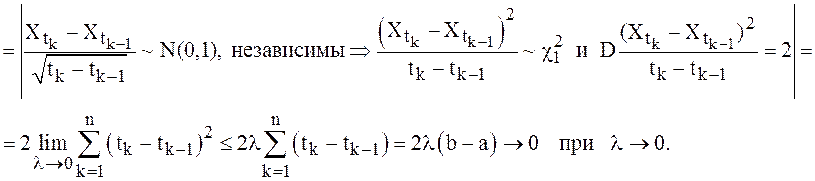
Определение 4.
Скалярная случайная функция X(t), ![]() , называется непрерывной
в среднем квадратическом или, короче, с.к. непрерывной в точке
, называется непрерывной
в среднем квадратическом или, короче, с.к. непрерывной в точке ![]() , если
, если
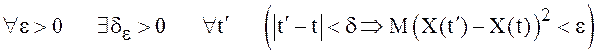 .
.
Если СФ X(t) с.к. непрерывна в любой точке ![]() , то она называется с.к. непрерывной в
области T.
, то она называется с.к. непрерывной в
области T.
Необходимое и достаточное условия с.к. непрерывности
СФ X(t), ![]() , можно выразить одним
из утверждений:
, можно выразить одним
из утверждений:
Теорема 1. Для
с.к. непрерывности СФ X(t) в области Т необходима и достаточна непрерывность
функции ![]() =
=![]() на
множестве Т
на
множестве Т![]() Т.
Т.
Теорема 2. Случайная функция X(t) с.к. непрерывна на области Т тогда и только тогда, когда
1)непрерывно на Т ее математическое ожидание ![]() и
и
2) непрерывна на области Т![]() Т ее
ковариационная функция
Т ее
ковариационная функция ![]() .
.
Справедливость теорем следует из определения функции, непрерывной в среднем квадратическом, и двух формулировок стохастического критерия Коши с.к. сходимости.
Пример 2. Покажем, что винеровский процесс является с.к. непрерывным.
Решение. Ковариационная
функция винеровского процесса ![]() ,
, ![]() , удовлетворяет требованиям теоремы 2.
, удовлетворяет требованиям теоремы 2.
Пример 3. Пусть
СФ X(t) задана на ![]() следующим образом:
следующим образом: 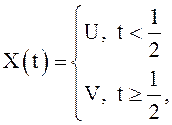 где U, V – независимые одинаково
распределенные случайные величины со средним m и дисперсией D>0. Исследовать
на непрерывность СФ X(t).
где U, V – независимые одинаково
распределенные случайные величины со средним m и дисперсией D>0. Исследовать
на непрерывность СФ X(t).
Решение. 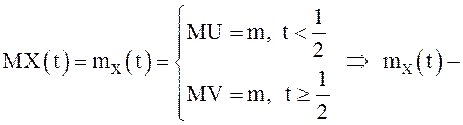 непрерывна на Т. Найдем теперь
непрерывна на Т. Найдем теперь ![]() . Если
. Если 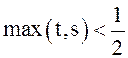 , то
, то ![]() . Аналогично,
. Аналогично, ![]() , если
, если 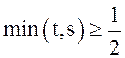 . Если же
. Если же 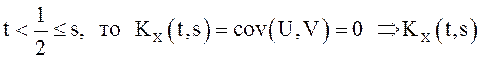 разрывна
в точке
разрывна
в точке ![]() , так как
, так как 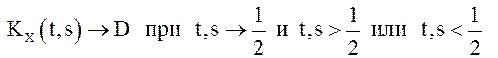 и
и 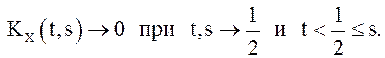
Замечание. Из условия с.к. непрерывности СП ничего нельзя сказать о непрерывности реализаций СП. Возможны самые различные комбинации: процесс с.к. непрерывен, но почти все его траектории разрывные функции, или же все траектории процесса непрерывные функции, сам же процесс не является с. к. непрерывным и т.д.
Определение 4.
Скалярная СФ X(t) называется с.к. дифференцируемой в точке ![]() , если существует такая случайная функция
, если существует такая случайная функция ![]() , к которой с.к. сходится при
, к которой с.к. сходится при ![]() случайная функция
случайная функция 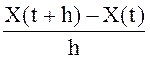 .
Случайная функция
.
Случайная функция ![]() называется с.к. производной
случайной функции X(t) в точке t.
называется с.к. производной
случайной функции X(t) в точке t.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.