Операции анализа над случайными функциями, страница 8

3.11.  Стохастические интегралы от случайных функций

Пусть W(t) – СПНП, ,  ,

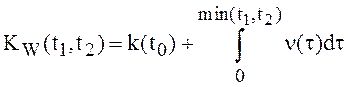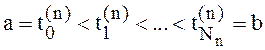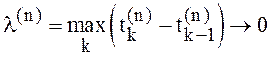- неотрицательная непрерывная функция и X(t) – с.к. непрерывная СФ с конечным моментом второго порядка, такая, что случайные величины  не зависят от  при любых N, M и ;  . Для любых разбиений отрезка  точками  с  при  запишем сумму

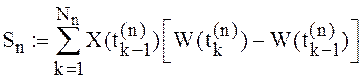,   n=1,2.

Определение 14. Стохастическим интегралом от СФ X(t) по процессу с независимыми приращениями W(t) (интегралом Ито) называется с.к. предел последовательности сумм , если он существует и не зависит от способа разбиения отрезка:

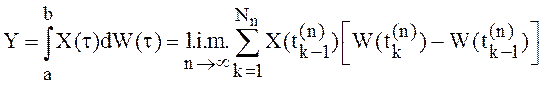                (18)

Замечание. 1).Значение СФ X(t) берется в левом конце отрезка 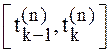.  При другом выборе точек из отрезка  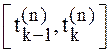значение предела изменится.

2). Стохастический интеграл от случайных функций также является частным случаем стохастических интегралов  по ортогональной стохастической мере, порожденной винеровскими процессами. 

Теорема 10. Необходимым и достаточным условием существования интеграла Ито является существование интеграла

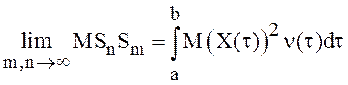,                           (19)

который согласно результатам п. 3.1  равен дисперсии интеграла

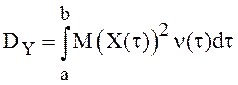.                                            (20)

Очевидно, что .

Пример 14. Найти дисперсию интеграла Ито 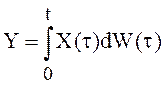, если X(t) – СФ с , , а W(t) – стандартный винеровский процесс.

Решение.    По формуле (20)

.

3.12.  Другие виды стохастических интегралов

от случайных функций

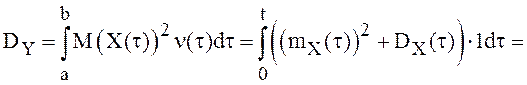
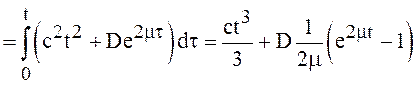Согласно замечанию к определению интеграла Ито, если брать значение функции в других точках отрезков 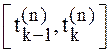, то будем получать другие интегралы. Так, если брать значения СФ X(t) в правых концах отрезков, то получим интеграл, обозначаемый символом :

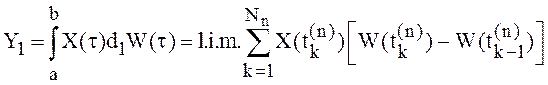       (21)

Для любого  можно определить стохастический -интеграл

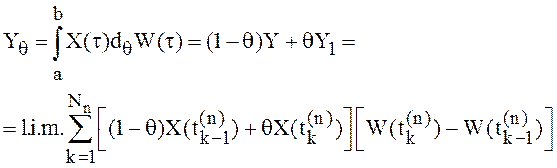      (22)

Интеграл Ито получается при , интеграл  - при ; при 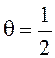 симметризованный стохастический интеграл носит название интеграла Стратоновича.

Среди всех этих интегралов интеграл Ито самый простой в вычислительном отношении – достаточно просто вычисляются математическое ожидание и дисперсия интеграла. При остальных   эти характеристики вычислять сложно из-за зависимости   с.в.  от с. в.  .

Как и в случае стохастических интегралов от неслучайных функций,   стохастические интегралы от случайных функций можно рассматривать как интегралы, содержащие белый шум.   Имея в виду формальное соотношение 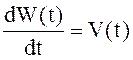, стохастический интеграл Ито можно записать  в виде: 

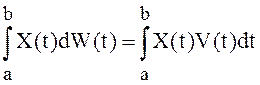                                          (23)

О процессе 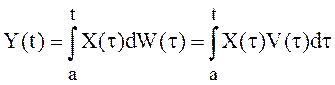    принято говорить, что он имеет стохастический дифференциал Ито (см. определение 7 п. 3.5.1) :

                                                                     (24)

Формула (24) представляет собой сокращенную форму записи интеграла (23).

Аналогичные сокращенные формы записей интегралов приняты и для других стохастических интегралов, в частности, для интеграла  принято обозначение  и  - для интегралов Стратоновича. В  случае же  произвольного - интеграла  пишут .

Так как процесс W(t) не имеет с.к. производной в обычном смысле, то   dW, а следовательно   и dY не являются дифференциалами в привычном смысле. Тем не менее равенство (24) имеет вполне определенный смысл. Поясним его.  Обозначим приращение случайной  функции Y(t) на малом интервале Δt через : , приращение процесса - : . Оценим порядок малости правой части полученного равенства для ΔY. Для этого вычислим условное математическое ожидание величины ΔΥ при данном значении x с. в. X(t) и условную дисперсионную матрицу. Сначала условное математическое ожидание:  =| по определению стохастического интеграла от случайных функций  являются независимыми случайными величинами при любых t | =. Теперь – условную дисперсионную матрицу: =|дисперсионная матрица с. в. ΔW(t) равна по определению процесса с независимыми приращениями    приближенно ν(t)Δt, где ν(t) – интенсивность процесса| ≈.  Следовательно, средние квадратичные значения компонент вектрора  ΔY имеют порядок малости . Таким образом,  в отличие от обычного дифференциала  функции и     с. к. дифференциала  случайной  функции, стохастический дифференциал имеет порядок малости .