Итак, выражение (32) дает общий вид решения уравнения (30).
1. Можно ли утверждать, что с.к. предел случайной функции обладает обычными свойствами предела неслучайной функции?
2. Можно ли утверждать, что с.к. предел последовательности с.в. обладает обычными свойствами предела последовательности?
3. Доказать, что линейная комбинация и произведение с.к. непрерывных на Т скалярных процессов – с.к. непрерывные на Т скалярные СП.
4.
Пусть ![]() - некоррелированные с.в. и
- некоррелированные с.в. и 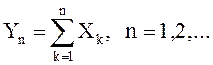 Доказать,
что последовательность
с.в.
Доказать,
что последовательность
с.в. ![]() сходится тогда и только тогда, когда
одновременно сходятся числовые ряды
сходится тогда и только тогда, когда
одновременно сходятся числовые ряды 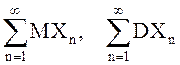 .
.
5.
Пусть ![]()
![]() скалярные СП, причем
скалярные СП, причем
![]() . Доказать,
что
. Доказать,
что ![]()
6.
Пусть ![]() - двумерный винеровский процесс, исходящий
из нуля, и
- двумерный винеровский процесс, исходящий
из нуля, и ![]() . Пусть
. Пусть ![]() -
некоторое разбиение отрезка . Доказать, что существует
-
некоторое разбиение отрезка . Доказать, что существует 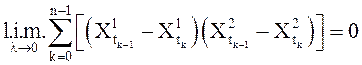 ,
где λ – мелкость разбиения отрезка.
,
где λ – мелкость разбиения отрезка.
7.
Будет ли с.к. дифференцируемым на Т случайный процесс ![]() - с.в., распределенная равномерно на
отрезке
- с.в., распределенная равномерно на
отрезке ![]() .
.
8.
Пусть ![]() - с.в., распределенная по равномерному
закону на отрезке
- с.в., распределенная по равномерному
закону на отрезке ![]() . Является ли: а) СП
. Является ли: а) СП ![]() , с.к. дифференцируемым? б) произвольная
реализация СП
, с.к. дифференцируемым? б) произвольная
реализация СП ![]() , дифференцируемой?
, дифференцируемой?
9.
Пусть ![]() , где
, где ![]() -
некоррелированные с.в. с
нулевыми математическими ожиданиями и одинаковыми дисперсиями, равными 0,1. Найти
м.о., дисперсию и ковариационную функцию СП
-
некоррелированные с.в. с
нулевыми математическими ожиданиями и одинаковыми дисперсиями, равными 0,1. Найти
м.о., дисперсию и ковариационную функцию СП ![]() .
.
10.
Найти ![]() , если
, если ![]() ,
, 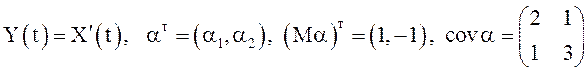 .
.
11.
Дифференцируемый в среднем квадратическом смысле СП ![]() ,
имеет м.о.
,
имеет м.о. ![]() и ковариационную функцию
и ковариационную функцию ![]() . Найти м.о. и ковариационную функцию СП
. Найти м.о. и ковариационную функцию СП ![]() .
.
12.
Пусть ![]() - стационарный в широком смысле СП, с.к. дифференцируемый
на Т. Является ли стационарным в широком смысле СП
- стационарный в широком смысле СП, с.к. дифференцируемый
на Т. Является ли стационарным в широком смысле СП ![]() ?
?
13.
Найдите одномерный закон распределения векторного СП ![]() ,
если
,
если ![]() - нормальный скалярный стационарный в широком
смысле СП с нулевым математическим ожиданием и ковариационной функцией
- нормальный скалярный стационарный в широком
смысле СП с нулевым математическим ожиданием и ковариационной функцией ![]() .
.
14.
Пусть ![]() , - скалярный стационарный в широком смысле
с.к. дифференцируемый на T процесс. Является ли стационарным в широком смысле
СП
, - скалярный стационарный в широком смысле
с.к. дифференцируемый на T процесс. Является ли стационарным в широком смысле
СП 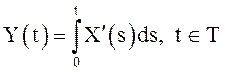 ?
?
15.
Пусть ![]() , - с.к. интегрируемый на T скалярный СП с известной
ковариационной функцией
, - с.к. интегрируемый на T скалярный СП с известной
ковариационной функцией ![]() . Найти взаимную ковариационную функцию
. Найти взаимную ковариационную функцию ![]() , если
, если 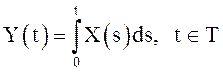 .
.
16. Ковариационная функция СП X(t)- ![]() ,
,
α, β>0. Определить дисперсию СП ![]() .
.
17. Задана ковариационная функция ![]() СП
СП ![]() . Пусть
. Пусть
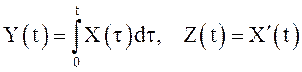 . Найти
. Найти ![]() .
.
18. Ковариационная функция СП X(t) имеет вид ![]() . Найти
. Найти
![]() , если
, если 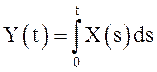 , а также
, а также ![]() ,
если
,
если ![]() .
.
19.
Случайная функция задана выражением 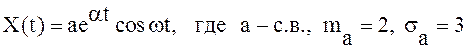 .
Найти м.о. и дисперсию случайной функции
.
Найти м.о. и дисперсию случайной функции 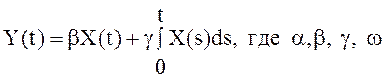 -
постоянные.
-
постоянные.
20. Показать, что если X(t) -
нормальный стационарный в широком смысле с.к. дифференцируемый СП, то процесс ![]() также нормальный стационарный в широком смысле. Найти
также нормальный стационарный в широком смысле. Найти ![]() , если
, если
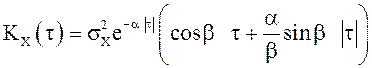 .
.
21. Является ли с.к. дифференцируемым винеровский процесс?
22.
Является ли СП ![]() , эргодическим по отношению к
м.о. , если
, эргодическим по отношению к
м.о. , если ![]() где
где ![]() имеет
нормальное распределение с параметрами
имеет
нормальное распределение с параметрами 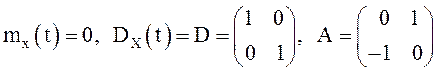 .
.
23.Пусть![]() - с.к. дифференцируемый на Т скалярный СП,
- с.к. дифференцируемый на Т скалярный СП,
![]() Найти
Найти ![]() ,
определить ее наибольшее значение. Будет ли СП
,
определить ее наибольшее значение. Будет ли СП ![]() эргодическим по отношению к его м.о.?
эргодическим по отношению к его м.о.?
24. Будет ли с.к. дифференцируемым и с.к. непрерывным пуассоновский процесс?
25.
Пусть ![]() - с. величина с
- с. величина с ![]() Найти
Найти
![]() , если
, если ![]() .
.
26.
Случайный процесс ![]() имеет математическое ожидание
имеет математическое ожидание ![]() ковариационную функцию
ковариационную функцию ![]() . Найти
. Найти ![]() если
если ![]() .
.
27.
Случайный процесс ![]() , имеет математическое ожидание
, имеет математическое ожидание ![]() ковариационную функцию
ковариационную функцию ![]() . Найти
. Найти ![]() если
если 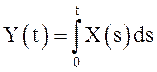 .
.
28.
Случайный процесс ![]() с. в. с математическим ожиданием
с. в. с математическим ожиданием
![]() дисперсией
дисперсией ![]() Найти
Найти ![]() если
если 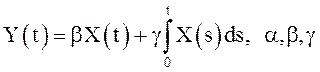 -
постоянные.
-
постоянные.
29.
Дифференцируем ли стационарный СП ![]() ?
?
30.
Сколько раз с.к. дифференцируем СП X(t) с ![]() ,
имеющей вид: а)
,
имеющей вид: а) ![]() б)
б) 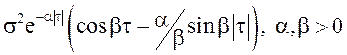 .
Записать
.
Записать ![]() , если она существует и найти дисперсии
процессов.
, если она существует и найти дисперсии
процессов.
31.
Показать, что ![]() стационарного СП
стационарного СП ![]() и его производной
и его производной ![]() удовлетворяет
условию:
удовлетворяет
условию: ![]() .
.
32.
Нормальный стационарный СП ![]() имеет
имеет ![]() Вычислить
Вычислить 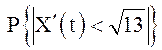 .
.
33.
Стационарный нормальный СП имеет ![]() . Найти двумерную
плотность совместного распределения вероятностей процессов
. Найти двумерную
плотность совместного распределения вероятностей процессов ![]() в один и тот же момент времени.
в один и тот же момент времени.
34.
СП ![]() - стационарный , с известной
ковариационной матрицей
- стационарный , с известной
ковариационной матрицей ![]() . Показать, что а)
. Показать, что а) 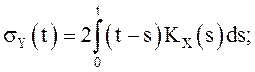 б)
б) 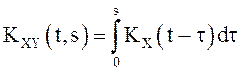 , если
, если
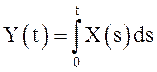 .
.
35.
Задана ![]() - ковариационная функция стационарного
процесса
- ковариационная функция стационарного
процесса ![]() . Найти
. Найти 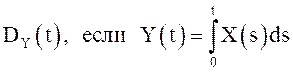 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.