В заключение отметим, что операция с.к. интегрирования
также не позволяет найти интеграл Y(t) в явном виде. Иногда это удается сделать
точно таким же способом, как и для получения с.к. производной. Пусть X(t)
такова, что все ее реализации интегрируемы по Риману на множестве Т, то есть 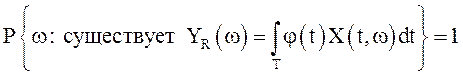 . Тогда
. Тогда ![]() -
случайная величина. Если X(t) к тому же с. к. интегрируем, то потраекторный
интеграл
-
случайная величина. Если X(t) к тому же с. к. интегрируем, то потраекторный
интеграл ![]() и с. к. интеграл
и с. к. интеграл 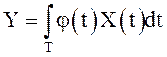 совпадают
с вероятностью 1. Рассмотрим пример.
совпадают
с вероятностью 1. Рассмотрим пример.
Пример 9.
Пусть ![]() и U и V – независимые гауссовские с.
величины с
и U и V – независимые гауссовские с.
величины с ![]() . Найти явный вид интеграла
. Найти явный вид интеграла 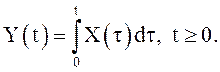
Решение. Для
любого ω траектория СФ X(t) имеет вид: ![]() и как
линейная комбинация интегрируемых функций интегрируема на любом конечном
отрезке
и как
линейная комбинация интегрируемых функций интегрируема на любом конечном
отрезке  (7)
(7)
Далее, СФ X(t) является при каждом t гауссовской с
параметрами ![]() . Условия теоремы 5 для функций
. Условия теоремы 5 для функций ![]() выполняются, поэтому с.к. интеграл Y(t)
существует и почти всюду равен правой части выражения (7), то есть
выполняются, поэтому с.к. интеграл Y(t)
существует и почти всюду равен правой части выражения (7), то есть 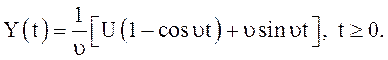 Его вероятностные характеристики имеют вид
Его вероятностные характеристики имеют вид
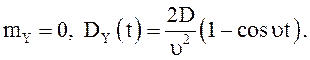
Введенные выше понятия с.к. производной и с.к. интеграла позволяют рассмотреть стохастические дифференциальные уравнения вида:
![]() ,
(8)
,
(8)
где
![]() - с.к. производная СП X(t), ξ(t) – с.к.
непрерывная при t≥0 случайная функция, A(t), B(t) – непрерывные неслучайные
функции,
- с.к. производная СП X(t), ξ(t) – с.к.
непрерывная при t≥0 случайная функция, A(t), B(t) – непрерывные неслучайные
функции, ![]() - некоторая случайная величина.
- некоторая случайная величина.
Уравнение (8) записывают в иной, эквивалентной форме:
![]() .
.
Определение 7.
СФ X(t), t≥0, является решением уравнения (8) с начальным условием ![]() , если при любом t≥0 выполнено соотношение
, если при любом t≥0 выполнено соотношение
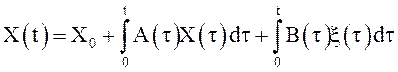 ,
(9)
,
(9)
где в правой части равенства (9) все интегралы понимаются в среднеквадратическом смысле.
С точки зрения определения (7) равенство (9)
эквивалентно равенству (8) в том смысле, что оба этих выражения определяют
один и тот же СП ![]() .
.
Можно проверить, что решением дифференциального
уравнения (8) или, что все равно, (9) является СП ![]() ,
имеющий вид
,
имеющий вид
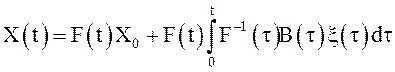 ,
(10) где
,
(10) где
![]() - решение уравнения
- решение уравнения
![]() (11)
(11)
Из теории ОДУ известно, что матричная функция ![]() из (11) такова, что
из (11) такова, что ![]() ≠0 при любом t≥0, а функция A(t) – кусочно
непрерывна.
≠0 при любом t≥0, а функция A(t) – кусочно
непрерывна.
Вычислим с.к. производную равенства (10) с учетом всех
свойств операций с.к. дифференцирования и интегрирования, отмеченных выше, 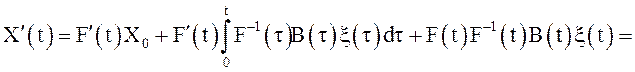
![]() | с
учетом формулы (11)|=
| с
учетом формулы (11)|=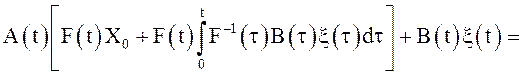 |с учетом формулы (10)| =
|с учетом формулы (10)| =![]()
Осталось проверить выполнение начального условия: ![]() В силу (11)
В силу (11) ![]() ,
следовательно, начальное условие выполняется.
Выражение (10) позволяет выписать явный аналитический вид решения
уравнения (8) во многих практически важных случаях.
,
следовательно, начальное условие выполняется.
Выражение (10) позволяет выписать явный аналитический вид решения
уравнения (8) во многих практически важных случаях.
Пример 10.
Пусть X(t), t≥0, удовлетворяет уравнению ![]() где
где ![]() образуют гауссовский случайный вектор,
причем
образуют гауссовский случайный вектор,
причем ![]() Найти закон распределения X(t) при любом
t≥0.
Найти закон распределения X(t) при любом
t≥0.
Решение.
Уравнение (11) для данного случая имеет вид ![]() Поэтому
Поэтому
![]() Общее решение уравнения, заданного в условии
задачи, согласно формуле (10) имеет вид
Общее решение уравнения, заданного в условии
задачи, согласно формуле (10) имеет вид 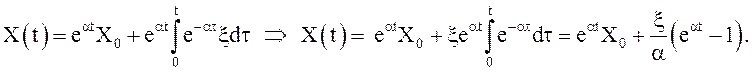
Видим, что как линейная комбинация гауссовских
случайных величин ![]() X(t)–гауссовская с. в. с
параметрами
X(t)–гауссовская с. в. с
параметрами 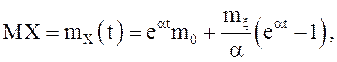
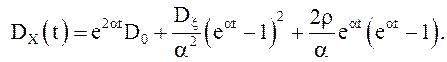
Определив с.к. дифференцирование и с.к. интегрирование на основе понятия с.к. сходимости последовательности случайных величин, мы приходим к понятию с.к. сходимости последовательности случайных функций.
Определение 7.
Последовательность СФ ![]() ,
, ![]() ,
называется сходящейся в среднем квадратическом смысле к СФ X(t),
если последовательность значений
,
называется сходящейся в среднем квадратическом смысле к СФ X(t),
если последовательность значений ![]() этих случайных функций с.к.
сходится к соответствующему значению
этих случайных функций с.к.
сходится к соответствующему значению ![]() случайной функции X(t)
при всех
случайной функции X(t)
при всех ![]() .
.
Случайная функция X(t)
называется с.к. пределом последовательности ![]() .
Пусть
.
Пусть ![]() - некоторый класс ограниченных функций
переменной t, каждая из которых отлична от нуля только в некоторой
конечной области (это существенно только если Т – бесконечная область).
- некоторый класс ограниченных функций
переменной t, каждая из которых отлична от нуля только в некоторой
конечной области (это существенно только если Т – бесконечная область).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.