Князьков А.Л. Основы радиоэлектронного наблюдения (Мониторинг электромагнитных излучений. Принципы и методы измерения углов прихода электромагнитных излучений РЭС), страница 4

При распространении в свободном пространстве поверхностями равных фаз являются концентрические сферы, в центре которых находится излучатель. Это сферическая волна. На больших расстояниях от работающего передатчика участок поверхности равных фаз сферической волны возле точки наблюдения можно считать  плоским и рассматривать волну как плоскую.

Структура поля безусловно искажается вблизи поверхностей раздела двух сред (земля – воздух), а также при наличии препятствий и вторичных излучателей: горы, деревья, здания и т.д.

Чтобы характеризовать направление векторов поля электромагнитной волны, вводится понятие поляризации, которое определяет  ориентацию электрического поля волны относительно плоскости распространения.

Плоскостью распространения называется плоскость, содержащая направление распространения и перпендикулярная к поверхности земли.

Имеют место следующие виды поляризации.

1.  Нормальная (вертикальная) поляризация. Вектор  напряженности электрического поля  лежит в плоскости распространения волны.

2.  Ненормальная поляризация. Вектор напряженности электрического поля   составляет некоторый угол с вертикальной относительно земли плоскостью, содержащей направление распространения. Частным случаем ненормальной поляризации является горизонтальная поляризация: вектор   - горизонтален, вектор  - вертикален.

При любой линейной поляризации электрическое поле можно  разложить на две составляющие – вертикальную и горизонтальную, совпадающие по фазе.

3. Если между вертикальной и горизонтальной составляющими имеется сдвиг фаз, то получается эллиптически-поляризованное поле. Вращение вектора    осуществляется неравномерно. Направление вращения зависит от разности фаз вертикальной и горизонтальной составляющих поля. Частным случаем эллиптической поляризации является круговая поляризация, которая имеет место, если сдвиг фаз между вертикальной и горизонтальной составляющей составляет  .

Для эллиптически поляризованной волны можно написать

,

,                                                        (2.1)

где   - орты, характеризующие направление большой и малой осей эллипса поляризации вектора  ,

 - величины большой и малой полуосей эллипса поляризации электрического и магнитного полей,

- волновое число, в свободном пространстве  ,

 - полярные координаты рассматриваемой точки, относительно начала координат,

- фаза в начале координат,

 - угол направления распространения волны с начальной линией отсчета (азимут, пеленг),

 - угол наклона фронта волны.

След плоскости распространения

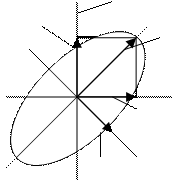
Рис. 2.1. Эллиптическая поляризация электрического поля.

Эллиптически поляризованную волну можно представить как сумму двух линейно поляризованных волн: в плоскости распространения  и перпендикулярно  ей 

,

 ,                                       (2.2) где  - единичный вектор, лежащий в плоскости распространения и перпендикулярный направлению распространения,

 - единичный вектор, перпендикулярный плоскости распространения,

 - соответствующие составляющие электрического и магнитного поля,

 - сдвиг фаз между нормально и ненормально поляризованными составляющими.

Угол, составляемый направлением большой оси эллипса поляризации с плоскостью распространения, называется углом поляризации   .

Анализируя выражения (2.2) для напряженности поля плоской волны видим, что направление вектора поля и фаза напряженности поля зависят от угла прихода волны.

Использование этих зависимостей позволяет осуществить радиопеленгование. Для определения направления вектора поля можно использовать электрический или магнитный диполь. Вращая диполь, получаем максимум  ЭДС в нем, когда его ось совпадает с направлением большой оси эллипса поляризации напряженности электрического и магнитного полей для электрического и магнитного диполей соответственно. Минимум  ЭДС получится, когда ось диполя параллельна малой оси эллипса поляризации. Однако  направление осей эллипса поляризации зависит не только от направления распространения, но и от углов наклона фронта волны и угла поляризации.