Князьков А.Л. Основы радиоэлектронного наблюдения (Мониторинг электромагнитных излучений. Принципы и методы измерения углов прихода электромагнитных излучений РЭС), страница 17

                                                 

      

              

Рис. 2.21. Прокладка пеленгов.

Из-за угловых погрешностей пеленгов в результате прокладки образуется многоугольник засечки, изображенный на рис. 2.21.

Обозначим угловые погрешности пеленгаторов , а среднеквадратические ошибки пеленгаторов  . Возьмем любой произвольный  j-й пеленгатор (рис. 2.22), поместим начало координат в точку  О  истинного положения пеленгуемого передатчика, направим ось  OX  вдоль параллели, а ось  OY – вдоль меридиана точки  О.

                                                                                y                          

             k    

O                    

x

       

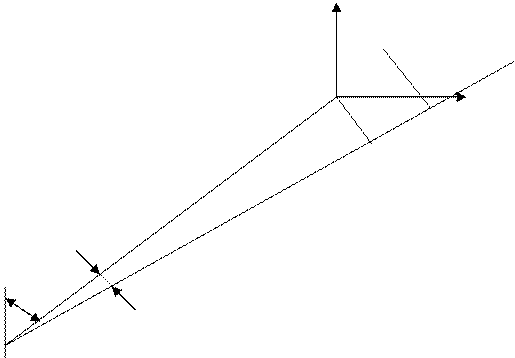
Рис. 2.22. К расчету плотности вероятности.

Обозначим   длину перпендикуляра из точки  О  до линии пеленга  , , где   - расстояние между точками   и  О.

Пусть в результате прокладки линий пеленгов на карте за местоположение передатчика принята точка  S  с координатами  (x,y), находящаяся на расстоянии    от линии пеленга  .

Найдем вероятность того, что расстояние от точки  S  до линии пеленга лежит в пределах от    до 

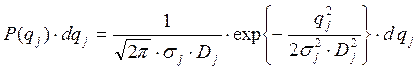,                                          где   - среднеквадратическое отклонение линии пеленга от истинного места передатчика.

Аналогичные выражения можно написать для других линий пеленгов. Вероятность того, что предполагаемое место передатчика  S  находится от   линий пеленгов, взятых из точек   на расстоянии от   до  , от   до  ,…, от  до 

 

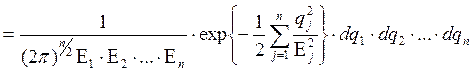.                            (2.25)

Координаты  наивероятнейшего месторасположения запеленгованного передатчика находятся методом наименьших квадратов из условия максимума выражения  (5.25)  или минимума показателя степени экспоненты

.                                                          (2.26) Для определения координат   следует приравнять нулю  производные по    и по   показателя степени экспоненты.

Точка   является наивероятнейшим местом нахождения передатчика и называется  центром  вероятности.

Геометрическим местом точек с одинаковой плотностью вероятности

                                                                        является эллипс с центром в точке  , то есть контуры постоянной плотности вероятности являются эллипсами с центрами в центре вероятности. Уравнение эллипса можно представить в виде

.                                                               (2.27) Коэффициенты  A, B и C находят по формулам

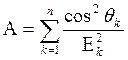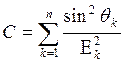,  ,  .                              (2.28)

Чтобы найти интегральную вероятность    нахождения передатчика внутри эллипса, построенного по заданному значению  , следует проинтегрировать выражение для дифференциальной плотности вероятности в пределах  площади эллипса

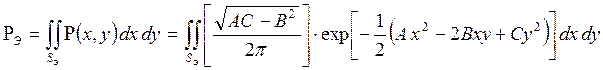.        После преобразований получим

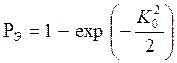,                                                                      (2.29) откуда находим

.                                                                      (2.30)

Зависимость  интегральной  вероятности   от коэффициента приведена на рис. 2.23. Если  , то получаем уравнение так называемого единичного эллипса , при этом  .

Совместим оси прямоугольной системы координат с главными осями эллипса вероятности. Уравнение эллипса принимает вид

,                                                                               где   и   - большая и малая полуоси эллипса.

                     100

80

60

40

20

0            1             2            3 

Рис. 2.23. Интегральная вероятность.

Можно рассчитать  ,  , площадь эллипса    и угол   между большой осью эллипса    и меридианом.

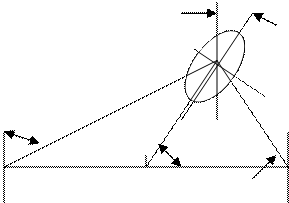
Рассмотрим простейший случай. Пусть у нас только два пеленгатора  .

                                                                         

O

N                              

                                                            

Рис. 2.24. Построение эллипса вероятности.

Для двух пересекающихся пеленгов площадь эллипса можно найти по формуле