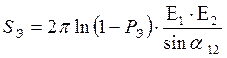Князьков А.Л. Основы радиоэлектронного наблюдения (Мониторинг электромагнитных излучений. Принципы и методы измерения углов прихода электромагнитных излучений РЭС), страница 18

,                                                          (2.31) где   - угол пересечения пеленгов.

Выражения для полуосей эллипсов находятся по формулам

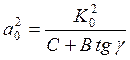,        .                                            (2.32) Угол    между большой осью эллипса   и меридианом определяется из выражения

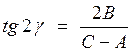,                                                                           (2.33) для двух пеленгаторов имеем

.                                     (2.34)

Известны различные графоаналитические способы определения параметров эллипса вероятности с использованием специальных планшетов и формул  (2.32) и (5.34) на расстояниях, где пеленги можно прокладывать в виде прямых линий.

Расчеты центра вероятности, размеров эллипса вероятности и ориентировки большой оси эллипса даны для случая плоской земли, то есть на расстояниях от радиопеленгаторов до 500 – 800 км. При больших дальностях необходимо считаться со сферичностью земли. Уравнения линий пеленгов должны быть соответственно  изменены. Если линии пеленгов проложены по карте с учетом сферичности земли, то центр вероятности и параметры эллипса вероятности могут быть рассчитаны по изложенной выше теории. 

Необходимо определить еще границы района, в пределах которого ошибка пеленгования с требуемой вероятностью не будет превосходить заданного значения. Площадь внутри границ этого района называется рабочей зоной двух радиопеленгаторов.

При заданной величине вероятности максимальным расстоянием, на котором может находиться пеленгуемый передатчик от его наивероятнейшего местоположения, является большая полуось эллипса вероятности.

Таким образом, определение района пеленгования при заданной максимальной линейной ошибке сводится к нахождению района, где большая полуось эллипса не превосходит заданной линейной ошибки.

Для расчета полуосей эллипса вероятности и угла ориентировки большой оси воспльзуемся формулами  (5.32) и (5.34).  Отрезок   (рис. 5.24) называется гониобазой  двух пеленгаторов. Обозначим угол между медианой ON и гониобазой  - , а длину медианы  .

Анализируя полученные выражения для различных местоположений пеленгуемого передатчика, находим, что для случая   и   (точка пересечения пеленгов находится на расстоянии полубазы от гониобазы), величины полуосей можно определить по формуле

,                                                         (2.35) то есть эллипс вероятности превращается в окружность с радиусом  .

Этот случай соответствует минимальной линейной погрешности, определяемой по формуле

.                                 (2.36)

Если пеленгуемый передатчик находится на одинаковом расстоянии от обоих пеленгаторов, равном длине базы , то радиус окружности равен  .

Рассмотрим способы построения рабочей зоны двух радиопеленгаторов. Обозначим заданную условиями эксплуатации максимальную допустимую линейную ошибку  при вероятности   через  . Условием для нахождения рабочей зоны пеленгаторов будет   при заданных значениях    и  .

Введем в формулу (5.36) такой параметр  Q, чтобы

.                                                        (2.37)

При заданных значениях   и  , а также  для рассматриваемых радиопеленгаторов можно рассчитать по (5.37)  Q, которое зависит от  .

Зная  Q и e  можно рассчитать зависимость   от  и получить исходные данные для построения рабочих зон двух пеленгаторов.

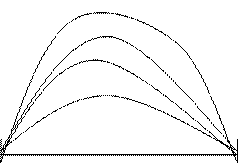На рис 2.25 построены контуры зон пеленгования для двух радиопеленгаторов при условии, что точности обоих пеленгаторов одинаковы. Границы зон симметричны относительно перпендикуляра к центру гониобазы  .

Рис. 2.25. Контуры зон пеленгования для двух радиопеленгаторов.

При равноточных  e = 1 пеленгаторах наибольшая дальность пеленгования, или наименьшая ошибка для любого расстояния от середины линии гониобазы, получается вдоль перпендикуляра к середине линии гониобазы.

Если точности пеленгаторов различны  , кривая рабочей зоны получается несимметричной.