Организационные вопросы обеспечения надежности радиоэлектронных средств при разработке, производстве и эксплуатации, страница 19

В работах [1,2] изложены основные законы и свойства (коммутативность, симметричность, законы де Моргана, свойства двойных отрицаний, свойства инверсно-идемпотентной обратимости  свойства единичной доминантности для  и ноль – доминантности для , согласованность относительно операции сложения  и др.) аддитивно - мультипликативной алгебры (АМ - алгебра) с базовыми операциями инверсии , вероятностного сложения  и умножения :

,                           (1)

,                                                      (2)

где  в общем случае являются действительными и (или) комплексными числами;

 есть символ вероятностного сложения .

Последние равенства в (I) и (2) показывают, что операции   и   связаны между собой через операцию инверсии срединного знака сложения (вычитания) на вычитание (сложение). Это означает, что базовые операции АМ - алгебра являются корнями квадратного уравнения 

,                                                         (3)

где +.

Расширение классов функций АМ - алгебры осуществляется через операцию суперпозиции.

Многоместные функции АМ – алгебры

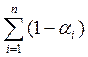,                                                                                                                           (4)

                                                                                            (5) связаны между собой преобразованиями (законами) де Моргана

, ,                                 (6)

где .

В формуле (4) символ  под знаком суммы означает, что суммирование производится по всем сочетаниям индексов .  Например, при   и  из (4) получим

,

Выражения (4) и (5) являются    - линейными формами, т.е. они являются линейными функциями по каждому своему аргументу . Соответственно (1) и (2) являются билинейными формами.

Согласно (6), в АМ - алгебре имеет место тождество

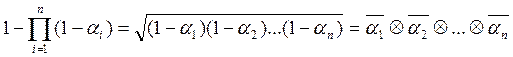 .                                      (7)

В АМ - алгебре имеют место следующие законы и свойства [1,2]: коммутативность, симметричность, законы де Моргана, свойства двойных отрицаний, свойство инверсно-идемпотентной обратимости , свойство согласованности относительно операции арифметического сложения .

Фундаментальными свойствами функций (4) и (5) являются свойства единичной доминантности и ноль - доминантности: если в (4) хотя бы одна из переменных  равна единице, то ; если в (5) хотя  бы одна из переменных равна нулю, то .

Дополнительно на интервале [0,1]  имеют место свойства концентрирования , реконцентрирования , субдистрибутивность , свойства вложенности

,  при .

Нетрудно усмотреть аналогию между свойствами многоместных базовых функций (4) и (5) АМ – алгебры и результирующими вероятностями безотказной работы параллельных и последовательных логических (структурных) схем надежности (ЛСН) устройств исистем (если положить, что  есть вероятности безотказной работы входящих в них элементов). Действительно, если в известной формуле 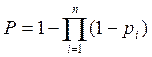 для параллельных ЛСН произвести перемножение биномов, то приходим к выражению (4). Соответственно вторая базовая операция (5) АМ - алгебры определяет надежность (вероятность безотказной работы) ЛСН с последовательной структурой.

Схемы с последовательной и параллельными структурами представлены соответственно на рис.1 и  рис.2.

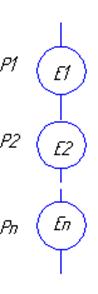
Рис.1

Рис.2

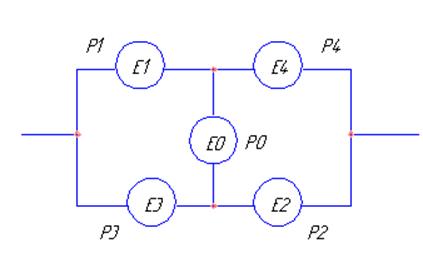
Рис.3

а)

б)

Рис. 4

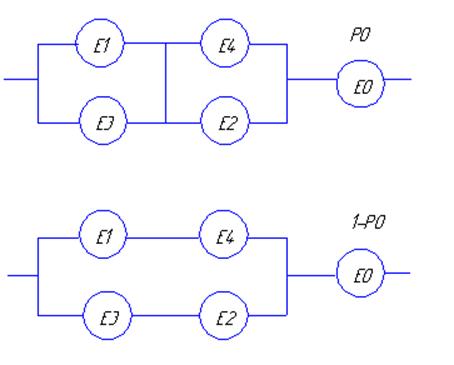
Для расчета надежности мостовых ЛСН их необходимо преобразовать в параллельно-последовательные структуры. Для этого используют метод расчленения исходной мостовой структуры по базовому (базовым) элементу (при взаимонезависимых отказах) [3]. Рассмотрим элементарную ЛСН с мостовой структурой, изображенную на рис.3. Расчленим ее на две схемы по базовому элементу , короткое замыкание или удаление которого превращает исходную схему в параллельно-последовательную структуру. Для этого в первой схеме положим , т.е. элемент  заменяется его коротким замыканием, а во второй схеме принимаем , т.е. элемент  удаляется. При этом в обоих стеках замещения элемент  включается последовательно с подученными структурами короткого замыкания (рис.4а) и холостого хода (рис.46) с присвоением ему вероятностей безотказной работы соответственно и . Надежность исходной ЛСН находится как сумма надекностей первой  и второй  схем: