Волны в плазме. Кинетический подход в изучении волн в плазме

Глава 5.         Волны в плазме

            Развитие колебаний и распространение волн в плазме является весьма существенным аспектом плазмодинамики. С возбуждением, нарастанием и затуханием волн связаны, в частности такие, важнейшие для приложений проблемы, как устойчивость плазмы, ее нагрев, неклассические механизмы переноса. Изучение волновых процессов проводится в рамках уже рассмотренных нами вкратце моделей представления плазмы.

5.1.Волны в холодной плазме в МГД приближении.

5.1.1.   Основные понятия и уравнения.

Холодной будем называть плазму, в которой выполняется условие:

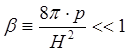, где - газокинетическое давление, а  - давление магнитного поля.

В случае выполнения неравенства влиянием тепловых эффектов можно пренебречь.

Если пренебрегать также столкновениями и другими процессами, проводящими к диссипации энергии, то такая модель называется приближением идеальной плазмы.

Теория колебаний плазмы заключается в совместном рассмотрении и уравнений движения проводящей среды, и уравнений Максвелла. Несколько преобразуем их. Применим  к обеим частям уравнения:

                                                       (5.1.1)

Получим

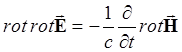
и подставим сюда уравнение, выражающее :

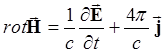                                                      (5.1.2)

После чего имеем

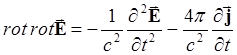
Используем известное соотношение векторного анализа

для преобразования двойного ротора, в результате чего получим волновое уравнение:

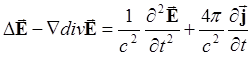                                                           (5.1.3)

Решение будем искать в виде в виде плоской волны:

                                                                 (5.1.4)

Где - комплексная амплитуда, w - круговая частота, k - волновое число.

Полезно сразу ввести следующие общие понятия:

Фазовая скорость волны

Групповая скорость

Связь w и k называется дисперсионным уравнением.

Показатель преломления

где c - скорость света.

Если фазовая скорость не зависит от частоты, то групповая скорость численно равна фазовой.

Чтобы определить U_ф и U_гр и по направлению, вводят волновой вектор , длина которого равна волновому числу, а направление определено таким образом, чтобы в плоской волне любая величина f зависела от координат и времени как

                                                          (5.1.4а)

Направление фазовой скорости есть направление волнового вектора, то-есть направление, в котором распространяется определенная фаза волны.

В анизотропной среде частота связана не только с величиной, но и с направлением волнового вектора, т.е. дисперсионные уравнения имеют вид:

где k₁, k₂, k₃ - составляющие волнового вектора.

В результате дифференцирования этого уравнения имеем:

U₁, U₂, U₃ имеют размерность скорости и рассматриваются как составляющие вектора групповой скорости. В векторной форме:

Символически это записывают следующим образом

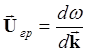
Направление U_гр - есть направление переноса энергии волной.Оси координат обычно выбирают так, чтобы k_z=0. Тогда k₁ - составляющая по нормали к магнитному полю, k₃ - вдоль поля.

В линейном приближении уравнения для комплексных амплитуд  имеют тот же вид, что и для f.

Для плоской волны дифференциальные операторы превращаются в алгебраические действия:

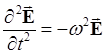
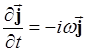
Тогда вместо имеем:

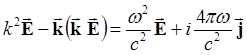                                  (5.1.5)

Таким образом, подставив в волновое уравнение (5.1.3) решение в виде плоской волны, мы получили дисперсионное уравнение (5.1.5), в котором влияние плазмы на волновой процесс учитывается, неопределенной пока, плотностью тока. Чтобы получить самосогласованную систему уравнений, нужнодобавить описание движения среды (плазмы) под действием поля.

Уравнения движения электронов и ионов без учета столкновений и других диссипативных процессов имеют вид: 

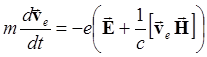                                            (5.1.6)

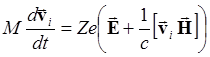                                           (5.1.7)

Ограничимся рассмотрением только линейных колебаний. Тогда d/dt можно изменить на ¶/¶t и в произведении  пренебречь собственным полем волны, т.е. изменить  на постоянное внешнее поле .

Преобразуем (5.1.6) и (5.1.7) так, чтобы получить уравнения для массовой скорости

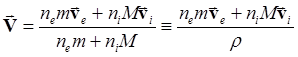                                                            (5.1.8)

и плотности тока

                                              (5.1.9)

здесь мы используем условие квазинейтральности

                                                                           (5.1.10)

будем пренебрегать массой электрона по сравнению с массой иона M>>m.

Просуммируем (5.1.6) и (5.1.7) с весами n_em и n_iM и получим

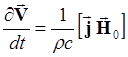                                                           (1.11)

Вычитание этих же уравнений с пренебрежением членами, содержащими М в знаменателе, дает

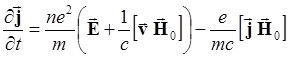                                     (5.1.12)

Система уравнений (5.1.11) - (5.1.12) совпадает с системой уравнений магнитной гидродинамики для идеального проводника, из которых выброшены силы давления. Если ввести обозначения