Волны в плазме. Кинетический подход в изучении волн в плазме, страница 8

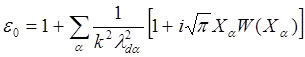
В данном случае мы должны учесть электронную компоненту плазмы и пучок-группу электронов, движущуюся относительно основной плазмы с некоторой средней скоростью. Поэтому выражение (5.3.24) трансформируется в:

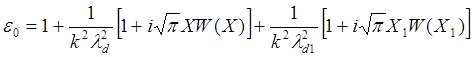                         (5.3.33)

где

;                             

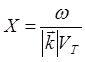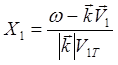
X – аргумент функции Крампа для электронной компоненты плазмы, X₁ – для электронов пучка, имеющих среднюю скорость V₁  (частота сдвинута в соответствии с допплеровским эффектом)и тепловой разброс, характеризуемый тепловой скоростью V_1T  

Исследуем вначале случай холодного пучка и холодной плазмы. Действуя аналогично подходу предыдущего параграфа и устремляя T в выражении, аналогичном (5.3.28) к нулю, получаем дисперсионное уравнение:

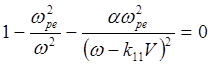                                        (5.3.34)

Здесь w_pe  -электронная ленгмюровская частота, a=n₁ / n₀  - отношение плотностей частиц пучка и плазмы, V  - скорость частиц пучка. Полагаем a <<1.

Учитывая малость параметра a и принимая, что k_ççV не слишком близко к w_{pe ,} находим, что два из четырех корней уравнения (5.3.34) соответствуют ленгмюровским колебаниям, а два других равны:

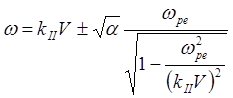                                  (5.3.35)

Из формулы (5.3.35) видно, что при корни комплексны и один из них соответствует колебаниям, нарастающим с инкрементом

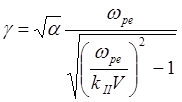                                          (5.3.36)

Эти колебания имеют групповую скорость, близкую к скорости частиц пучка  и поэтому называются сносовыми. Если частота таких сносовых колебаний приближается к ленгмюровской, то-есть k_ççV»w_pe уравнения (5.3.35) и (5.3.36) теряют силу и (5.3.34) нужно исследовать другим способом.

Итак, полагаем, что в нулевом приближении частота колебаний близка к ленгмюровской:

                                                            (5.3.36)

и поправка к частоте по абсолютной величине сильно превышает разницу между ленгмюровсой частотой и k_ççV :. Тогда из (5.3.34) следует:

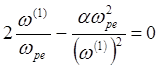                                            (5.3.37)

Отсюда получаем выражения для действительной и мнимой частей добавки к частоте нарастающих колебаний:

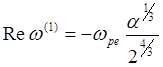                                           (5.3.38)

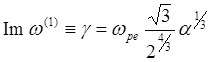                                  (5.3.39)

На границе применимости этих формул, выражения (5.3.36) и (5.3.39)дают близкие значения для инкремента нарастания колебаний. Следует отметить, что из-за пропорциональности инкремента кубическому корню из отношения плотности пучка к плотности плазмы, даже при малых плотностях пучка инкремент нарастания колебаний может быть значительным. Физическая природа такого относительно большого нарастания волн заключается в резонансе ленгмюровских плазменных колебаний основной плазмы и сносовых колебаний в пучке.

Оценим теперь влияние теплового разброса скоростей частиц на развитие колебаний, раскачиваемых пучком. Вернемся к дисперсионному уравнению(5.3.33). Как мы уже отмечали, приближению холодной плазмы соответствует случай . Поэтому общий критерий применимости этого приближения к данной задаче может быть записан в виде:

В случае пучка малой плотности ограничения на тепловой разброс более плотной компоненты состоит в требовании существенного превышения скоростью пучка средней скорости теплового движения

в то время как для менее плотной компоненты это требование оказывается более жестким:

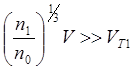
Чтобы получить критерии более точные, чем сильные неравенства, нужно рассмотреть конечные значения аргумента x . При этом, с точностью до членов  включительно, имеем:

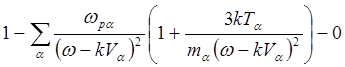                       (5.3.40)

Из (5.3.40) можно найти максимальный (резонансный) инкремент колебаний, возбуждаемых «слегка нагретым» пучком в «слегка нагретой» плотной плазме:

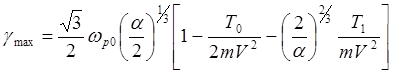              (5.3.41)

Сравнивая (5.3.41) и (5.3.39) можем сделать вывод о тои, что приближение холодной плазмы дает правильный по порядку величины результат даже когда приведенные выше неравенства не являются сильными.

Физический смысл приведенных критериев заключается в требовании, чтобы среднее тепловое смещение частиц за характерное время (период колебаний, либо время обратного инкремента) , измеренное в системе координат, движущейся с пучком, не должно превышать длину волны.