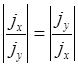Волны в плазме. Кинетический подход в изучении волн в плазме, страница 4

     т.е.                                           (5.1.47)

Амплитуда тока одинакова во всех направлениях , что из-за (5.1.36) относится и к амплитуде . В течение цикла, меняется лишь фаза волны, т.е. она вращается вокруг направления . Такие волны называются волнами с круговой поляризацией. Два знака в (5.1.46) соответствуют вращению в противоположных направлениях.

Одна из них может существовать лишь при  - это обыкновенная волна. Вторая лишь при - необыкновенная. У первой  вращается в сторону вращения ионов в магнитном поле, у второй - в сторону электронного вращения.

5.1.6.Магнитный звук.

Рассмотрим теперь волны, распространяющиеся перпендикулярно магнитному полю. В этом случае, как и ранее, волна, поляризованная вдоль отщепляется (это электромагнитная волна) и достаточно рассмотреть волны с плоскостью поляризации . Пусть ось х - вдоль направления распространения , z -  вдоль , y^ к этим направлениям. Тогда составляющие уравнения (1.5) по х и y примут вид:

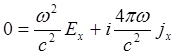                                                (5.1.48)

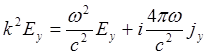                                          (5.1.49)

Выразив отсюда E_x и E_y  и подставив в (5.1.18) получим

                          (5.1.50)

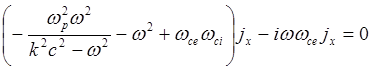                     (5.1.51)

Здесь амплитуды E_x и E_y, j_x и j_y не одинаковы, т.е. волна имеет эллиптическую поляризацию. Дисперсионное соотношение получаем приравнивая нулю определитель системы (5.1.50) - (5.1.51) .

Вновь рассмотрим предельную область очень низких частот.

                                                          (5.1.52)

Пусть также N>>1, т.е. скорость распространения волны мала по сравнению со скоростью света  (сильно влияние плазмы, можно пренебречь токами смещения),:

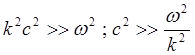                                              (5.1.53)

В этом случае из (6.3) следует

                                                         (5.1.54)

и из системы (6.1) - (6.2)

                                                     (5.1.55)

т.е. в этой области эллиптическая волна вырождается в линейно поляризованную. Приближенное дисперсионное соотношение для этой области можно получить, рассматривая лишь (5.1.51):

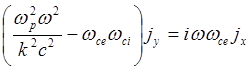                                            (5.1.56)

С учетом (6.7) ясно, что коэффициент при j_y должен быть мал, т.е. дисперсионное соотношение в этой области частот стремится к

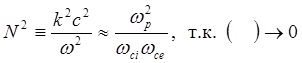              (5.1.57)

Что совпадает с (5.1.39). Это значит, что при низких частотах волны в плазме распространяются как параллельно, так и перпендикулярно магнитному полю с одной и той же скоростью - альфвеновской (см. (5.1.41)). Однако здесь другая природа волн. Там это поперечные, электромагнитные волны. Здесь процесс колебаний можно рассматривать как сжатие и расширение плазмы вместе с вмороженным в нее магнитным полем. Это похоже на распространение звука. Поэтому и называется магнитным звуком. Вместо газового давления здесь действует магнитное давление .

Если в обычную для скорости звука формулу

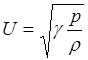
вместо p подставить  , взяв g_м =2 для вмороженного поля, то получится

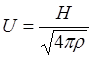, что совпадает с формулой (5.1.41).

5.2.      Волны в горячей плазме в МГД приближении.

5.2.1.  Основные уравнения.

В этой модели учитывается давление частиц. Принимают, что электронное давление действует на электроны, ионное ‑  на ионы, а взаимодействие между этими двумя жидкостями описывается электрическим сопротивлением плазмы. Идеальная проводимость – отсутствие взаимодействия между ионами и электронами.

Уравнения движения электронов и ионов в линейном гидродинамическом приближении без взаимодействия:

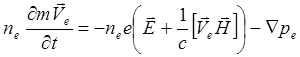                        (5.2.1)

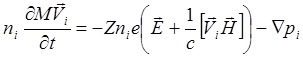                       (5.2.2)

Полные производные заменены частными в силу линейного приближения. Если сложить (5.2..1) и (5.2..2), то с учетом

                                                             (5.2.3)

и определения плотности тока

                                                  (5.2.4)

то получится для массовой скорости

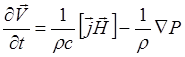                                             (5.2.5)

где

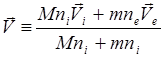– массовая скорость                             (5.2.6)

и

–массовая  плотность                                   (5.2.7)

если разделить (5.2.1) на , а (5.2.2) на  и вычесть (5.2.1) из (5.2.2), выбросив члены с  в знаменателе (т.е. считая ионы неподвижными) то получим уравнение идеальной проводимости