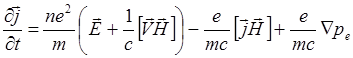Волны в плазме. Кинетический подход в изучении волн в плазме, страница 5

                                       (5.2.8)

Для учета джоулевой диссипации в правую часть добавляют член . Тогда получается обобщенный закон Ома с учетом электронного давления

                                                                                                                         (5.2.9)

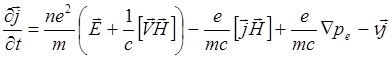где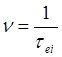

Неточность описания плазмы с помощью (5.2.1)– (5.2.8):

а) не учитывается анизотропия давлений – в разреженной плазме давление может быть не скаляром, а тензором. Это часто неважно.

б) не описывается бесстолкновительная диссипация. Это может привести к тому, что некоторые типы колебаний, получающтеся в гидродинамическом приближении не на самом деле реализуются.

5.2.2.   Скорость звука.

Чтобы описать влияние давления на волновые движения нужно связать  со скоростью движения вещества.

Пренебрегая диссипативными процессами, считаем, что состояние вещества меняется по адиабатическому закону

                                                            (5.2.10)

откуда

                                              (5.2.11)

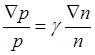                                                    (5.2.12)

Запишем ещё уравнение непрерывности

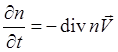                                                (5.2.13)

в линейном приближении это сведется к

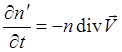                                                (5.2.14)

– возмущенная концентрация, . Что для плоской волны вида

даст 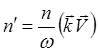                                                                                            (5.2.15)

Если невозмущенная плотность  – постоянна в пространстве, то

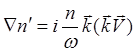                                          (5.2.16)

и тогда, из (5.2.12) следует

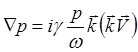                                          (5.2.17)

Это уравнение решается совместно с уравнением движения. Поскольку взаимодействием ионов и электронов мы пренебрегаем, уравнения(5.2.11) – (5.2.17) могут применяться отдельно к ионам и электронам, и меняются при этом независимо.

Для газа из нейтральных частиц (5.2.17) решается совместно с линеаризованным уравнением Эйлера

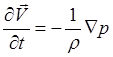                                                 (5.2.18)

которое для плоской волны дает

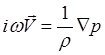                                                  (5.2.19)

Выразив отсюда , подставим его в (5.2.17) и, для продольных  волн получим дисперсионное уравнение

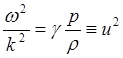(5.2.20)

Здесь – обычная скорость звука. По аналогии удобно ввести ионную и электронную скорости звука

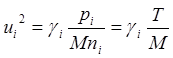                                                 (5.2.21)

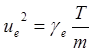                                                                 (5.2.22)

где и – температуры ионов и электронов в энергетических единицах.

Тогда (5.2.12) для i и e можно записать

                                               (5.2.23)

                                              (5.2.24)

а (5.2.17) в виде

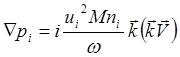                                   (5.2.25)

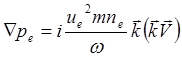                                    (5.2.26)

Пусть в плазме могут распространяться обычные звуковые волны, для которых можно пренебречь разделением зарядов и эл. токами. Это значит, что электроны и ионы должны иметь одинаковые средние (упорядоченные) скорости

                                                      (5.2.27)

Тогда сложение (5.2.25) и (5.2.26) дает (с учетом ) для общего давления

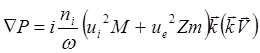                               (5.2.28)

Это можно записать в виде аналогичном (5.2.25)

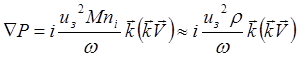                        (5.2.29)

если определить скорость звука соотношением

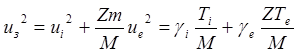                      (5.2.30)

Это – так называемая скорость ионного звука. Она определяется суммарной  и массой ионов.

5.2.3.Плазменные волны и ионный звук.

Рассмотрим вначале продольные волны без магнитного поля. У этих волн т.е.

Уравнения движения (5.2.1) и (5.2.2) для продольных волн без магнитного поля с учетом (5.2.25) и (5.2.26) принимают вид

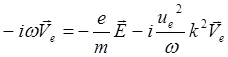                                                  (5.2.31)

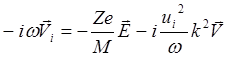                                                  (5.2.32)

Отсюда видно, что в данном случае и . Эти уравнения решаются совместно с уравнением

                                                                           (5.2.33)

где

                                                                      (5.2.34)

В (5.2.34) входят только возмущения концентраций, т.к. невозмущенное . Отсюда для продольных волн