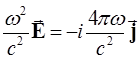Волны в плазме. Кинетический подход в изучении волн в плазме, страница 3

                                                   (5.1.28)

что с учетом (5.1.27) дает

                                                              (5.1.29)

Это означает, что колебания, поляризованные вдоль магнитного поля и распространяющиеся вдоль него, являются электростатическими плазменными колебаниями.

Для волн, бегущих поперек магнитного поля, но поляризованных вдоль него, вместо (5.1.5) имеем:

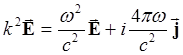                                         (5.1.30)

Это при подстановке (5.1.27)дает дисперсионное соотношение:

                                                     (5.1.31)

такое же, как для описания распространения электромагнитных волн в плазме без магнитного поля.Так же выглядит и квадрат показателя преломления:

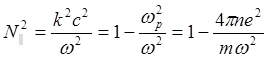                           (5.1.32)

Эту величину можно рассматривать как продольную диэлектрическую проницаемость плазмы. Без магнитного поля диэлектрическая проницаемость плазмы изотропна и по любому направлению дается выражением (5.1.32).

5.1.4.Альфвеновские волны.

            Рассмотрим волны, распространяющиеся вдоль магнитного поля при произвольной поляризации. Вновь разложим ее на две независимые друг от друга составляющие: с продольной и поперечной поляризацией относительно магнитного поля. Волна с продольной поляризацией (т.е. с направлением электрического поля вдоль направления распространения волны и, в данном случае, также вдоль магнитного поля) вырождается в продольные колебания на плазменной частоте, уже рассмотренные нами. Здесь нас интересует другая компонента: волна бегущая вдоль магнитного поля с поперечной поляризацией. Для такой волны

                                                (5.1.33)

и (5.1.5) сведется к виду

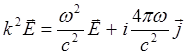                                (5.1.34)

Можно еще больше упростить полученное выражение, если пренебречь первым членом в правой части (5.1.34). Это будет означать, что ток, переносимый частицами велик по сравнению с током смещения, т.е. влияние плазмы на распространение волны велико (показатель преломления много больше единицы, ситуация сильно отличается от случая распространения волны в вакууме):

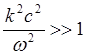                                                   (5.1.35)

Тогда из(5.1.34) следует

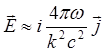                                              (5.1.36)

Отсюда видно, что ток направлен по электрическому полю, которое перпендикулярно к магнитному. Поэтому уравнение (5.1.18) преобразуется к следующему виду:

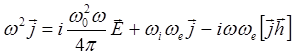                                     (5.1.37)

Подставив в (5.1.37) электрическое поле, даваемое (5.1.36), получим

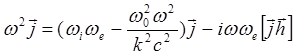                                    (5.1.38)

Исследуем дисперсионное уравнение (5.1.38) в области низких частот.Если

                                                     (5.1.39)

оно существенно упростится:

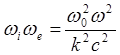                                              (5.1.39)

При этом показатель преломления и фазовая скорость волны выразятся соотношениями:

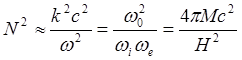                             (5.1.40)

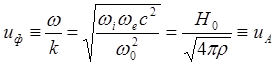                      (5.1.41)

где - массовая плотность плазмы. - альфвеновская скорость. Сами волны этого типа называются альфвеновскими. Они могут быть наглядно интерпретированы как поперечные колебания вмороженных в плазму силовых линий магнитного поля вместе с плазмой. Скорость их распространения постоянна (дисперсии нет)

5.1.5. Дисперсия вблизи циклотронных частот.

Если (5.1.39) не выполнено, то возникает дисперсия и проявляются гиротропные свойства плазмы. Распишем (5.1.38) в проекциях, имея в виду, что  :

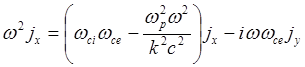                                              (5.1.42)

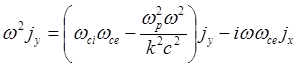                                                (5.1.43)

Дисперсионное уравнение получается приравниванием нулю определителя этой системы, что проще сделать, выразив отношение амплитуд:

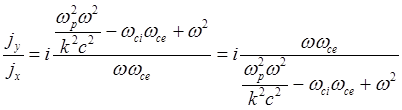                           (5.1.44)

откуда

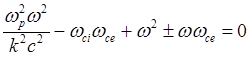                                                         (5.1.45)

или

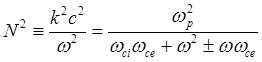                                                       (5.1.46)

Знаменатель обращается в нуль при двух резонансных частотах (или частотах аномальной дисперсии). Если не пренебрегать при выводе m_e по сравнению с M, то эти частоты в точности равны . Из (5.1.46) получаются значения очень близкие к ним (с точностью до величин порядка  опущенных при выводе (5.1.12) ).

Из (5.1.44) следует