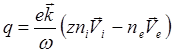Волны в плазме. Кинетический подход в изучении волн в плазме, страница 6

                                                             (5.2.35)

Этот результат – закон сохранения электрического заряда

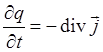                                                                           (5.2.36)

Подстановка (5.2.35) в (5.2.36) дает для продольной плоской волны

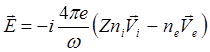                                                           (5.2.37)

или с учетом квазинейтральности (5.2.3)

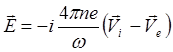                                                             (5.2.38)

подстановка (5.2.38) в (5.2.31) и (5.2.32) дает

                                          (5.2.39)

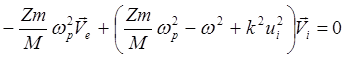                          (5.2.40)

определитель этой системы дает дисперсионное соотношение для продольных волн в плазме без магнитного поля

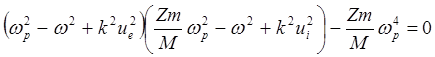                    (5.2.41)

Здесь  – электронная плазменная частота.

Заметим, что

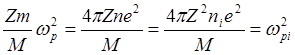                                    (5.2.42)

Расположим уравнение (5.2.41) по степеням частоты

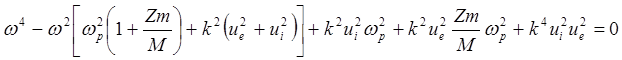(5.2.43)

Это уравнение определяет две различные ветви колебаний. Высокочастотная или электронная ветвь получается если пренебречь свободным членом. Тогда

                                                        (5.2.44)

Практически , поэтому

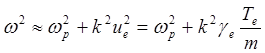                                        (5.2.44а)

В (5.2.44а) входят величины, относящиеся только к электронам. Поэтому это – электронная ветвь.

Ионная ветвь получается, если пренебречь . Тогда дисперсионное соотношение

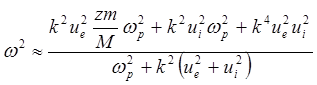                                (5.2.45)

Для длинных волн (5.2.45) стремится к

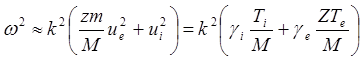                       (5.2.46)

Это отвечает скорости распространения  ионного звука.

Для коротких волн

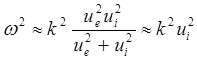                                                        (5.2.47)

т.к.

5.3.Кинетический подход в изучении волн в плазме.

5.3.1.  Дисперсионное уравнение в кинетике в отсутствии магнитного поля.

Рассмотрим получение дисперсионного уравнения в кинетике на простейшем примере : изучаются продольные высокочастотные колебания без внешнего магнитного поля. Считая частоту достаточно высокой, чтобы исключить из рассмотрения ионную компоненту, запишем кинетическое уравнение только для электронов:

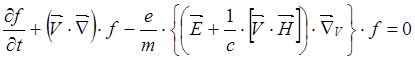              (5.3.1)

В линейном приближении: , — равновесная по отношению к рассматриваемому процессу функция распределения. Пусть —однородна и постоянна во времени, тогда из (5.31):

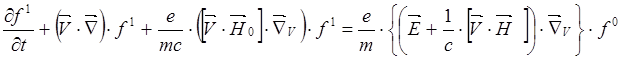(5.3.2)

—внешнее магнитное поле; —собственное поле волны. Рассматриваем плоскую волну:

 происходит только от вихревого электрического поля, так как: 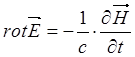. В плоской продольной волне электрическое поле безвихревое (потенциальное). зависит только от x. Поэтому  и уравнение (2) упрощается:

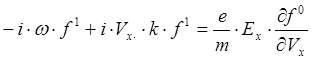                                   (5.3.3)

Электрическое поле находим из:

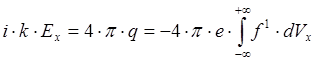                                  (5.3.4)

(так как , то  не вносит вклад в плотность заряда—реально это означает квазинейтральность плазмы в равновесном состоянии). Чтобы получить дисперсионное соотношение нужно из (5.3.3) выразить  через  и подставить в (5.3.4):

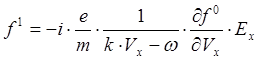                               (5.3.5)

подставив это в (5.3.4), получим:

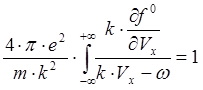                                          (5.3.6)

Это и есть дисперсионное уравнение. Удобнее ввести нормированную функцию распределения , определенную из:

, то есть 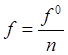                                      (5.3.7)

где —полная концентрация электронов.

Условие на  тогда:

                                                                 (5.3.8)

При этом (5.3.6) перепишется:

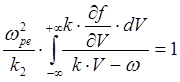                                                (5.3.9)

Имея в виду, что  при , преобразуем интеграл, беря его по частям:

 .

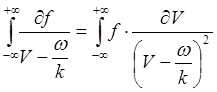Получим дисперсионное соотношение в виде:

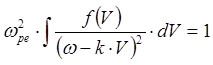                                         (5.3.10)

иногда это удобнее.

Если —холодная плазма, неподвижная, то из (10) имеем:

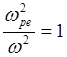—электронные ленгмюровские колебания.

Интеграл в (5.3.9) можно вычислить, заменив в знаменателе  на , где —бесконечно малое положительное число.

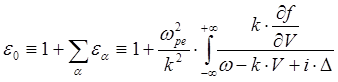                          (5.3.10а)

используя соотношение:

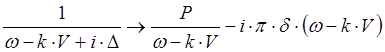                    (5.3.11)

диэлектрическую проницаемость можно представить в виде:

                                (5.3.12)

где

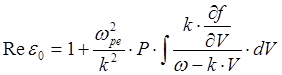                                     (5.3.13)

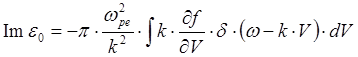                     (5.3.14)