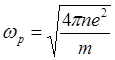Волны в плазме. Кинетический подход в изучении волн в плазме, страница 2

                                                  (5.1.13)

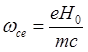                                                       (5.1.14)

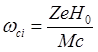                                                     (5.1.15)

то (5.1.12) перепишется

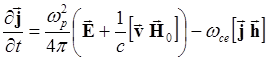                                          (5.1.16)

где - единичный вектор в направлении постоянного внешнего магнитного поля. Для плоской волны вида (5.1.4) уравнения (5.1.11) и (5.1.16) принимают вид:

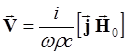                                                 (5.1.17)

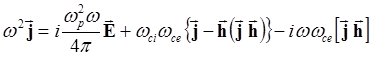                     (5.1.18)

Здесь w - круговая частота возмущения.

В последнем уравнении раскрыто двойное векторное произведение по формуле             и использовано соотношение

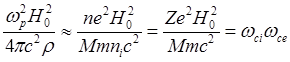                                    (5.1.19)

Теперь рассмотрение всех типов колебаний холодной плазмы сводится к совместному решению уравнений (5.1.5), описывающего возмущения полей, и (5.1.18)., описывающего движение плазмы и представляющего собой нечто вроде обобщенного закона Ома.

Повторим допущения, сделанные  при их выводе:

·  Амплитуды всех переменных в волне малы - линейное приближение, что дает возможность пренебречь квадратичными членами;

·  Тепловое давление мало (приближение холодной плазмы);

·  Пренебрегается диссипативными эффектами (идеальная плазма);

·  Отброшены члены ~ m/M.

5.1.2.Волны при отсутствии магнитного поля.

            Начнем рассмотрение с наиболее простого случая. Пусть внешнее магнитное поле плазме отсутствует :H₀ = 0              

При этом (5.1.18) сводится к простому виду:

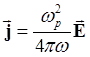                                                       (5.1.20)

Из (5.1.5), в свою очередь, получаем

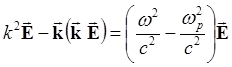                                     (5.1.21)

Произвольную волну можно разложить на две независимые: Продольную  и поперечную . Для продольной   и из (2.2) (5.1.21) следует:

                                                  (2.3) (5.1.22)

Это плазменные колебания на фиксированной частоте - такие только и возможны в холодной плазме.

Для поперечных  и из (5.1.21) получаем:

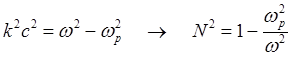   (2.4)

Соотношение(5.1.23)- дисперсионное уравнение для распространения электромагнитных волн в плазме без магнитного поля. Пока выполняется условие распространение волны возможно. Если же частота колебаний в волне становится меньше плазменной частоты, волновое число и показатель преломления становятся мнимыми, т.е. волна отражается от границы плазмы.

Фазовая скорость выражается следующей формулой:

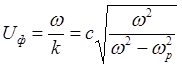                                               (5.1.24)

В области распространения волны то-есть при частотах. превышающих плазменную, фазовая скорость больше скорости света  и стремится к бесконечности при , Групповая скорость:

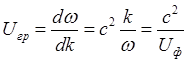                                            (5.1.25)

Откуда непосредственно следует:

                                                               (5.1.26)

При частотах много больших плазменной волна распространяется как в вакууме (влияние плазмы мало) и обе скорости стремятся к скорости света. При усилении влияния плазмы (при приближении частоты к плазменной) фазовая скорость, как мы видели, стремится к бесконечности, а групповая, как это следует из соотношения (5.1.26), стремится к нулю. Групповая скорость всегда остается меньше скорости света.

5.1.3.Волны при наличии магнитного поля – простейшие случаи.

Система (5.1.5) – (5.1.18) очень сложна для анализа при произвольном направлении распространения волн. Рассмотрим пробные случаи.

Возьмем составляющую векторного уравнения (5.1.18) вдоль поля. Так как. , то

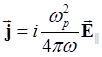                                                    (3.1)(5.1.27)

Составляющая уравнения (5.1.5) вдоль магнитного поля не, содержит  в двух случаях: при распространении волны вдоль поля и при распространении ее поперек поля, когда .

В этих двух простейших случаях колебания с электрическим полем, параллельным магнитному, отщепляются, т.е. представляют собой независимые ветви колебаний - магнитное поле на эти ветви не действует. В гидродинамике это утверждение точное. В кинетике, вообще говоря, есть особенности вблизи циклотронных частот и их обертонов. Но, если от этого отвлечься, то такие колебания распространяются вдоль магнитного поля так же, как и в его отсутствие. Действительно, для колебаний с , (5.1.5) сводится к виду: