Волны в плазме. Кинетический подход в изучении волн в плазме, страница 7

где—главное значение интеграла. Отсюда следует, что —комплексна, если при 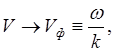 отлична от 0. При комплексном  комплексна и частота собственных колебаний плазмы. Мнимую часть частоты собственных колебаний легко найти, когда она мала по сравнению с вещественной, что возможно при малом . Действительно, при  мнимую добавку к частоте достаточно учесть только в функции .

Разлагая ее по степеням :

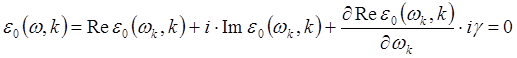    (5.3.15)

откуда следует выражение для действительной и мнимой части частоты колебаний:

                                                         (5.3.16)

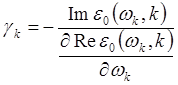                                              (5.3.17)

здесь ;

5.3.2.  Диэлектрическая проницаемость максвелловской плазмы

Рассмотрим случай максвелловской функции распределения частиц

 плазмы по скоростям:

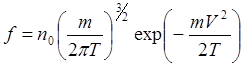                                  (5.3.18)

Подставив (5.3.18) в выражения для действительной и мнимой частей диэлектрической проницаемости, полученные в предыдущем параграфе (5.3.13) и (5.3.14), получим:

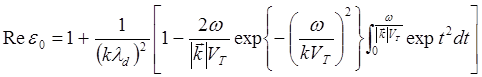                       (5.3.19)

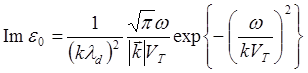                                                          (5.3.20)

Здесь 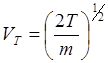 - тепловая скорость, 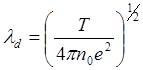- дебаевский радиус. Эти выражения получены для вещественных w. Их аналитическое продолжение на область комплексных wсводится к простой замене вещественных wна комплексные. Объединяя их, находим, что при любом комплексном w  диэлектрическая проницаемость максвелловсой плазмы имеет вид:

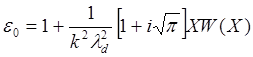                                             (5.3.21)

где ;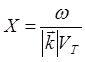             

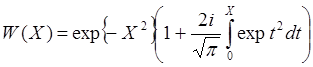
W(X) – интеграл вероятности от комплексного аргумента, называемый также функцией Крампа. Эту функцию можно аппроксимировать следующими приближенными выражениями, удобными при аналитическом подходе к исследованию дисперсионных уравнений:

При

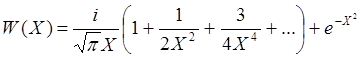;                                             (5.3.22)

При

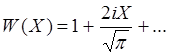                                                                                     (5.3.23)

При наличии многокомпонентной плазмы в выражении (5.3.21) для  следует в «плазменном слагаемом» учесть сумму по компонентам:

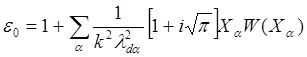                                   (5.3.24)

a - сорт частиц (электроны, ионы)

5.3.3.  Бесстолкновительное затухание плазменных волн (затухание Ландау).

Будем исходить из общего выражения для диэлектрической проницаемости для плазмы с максвелловским распределением электронов по скоростям

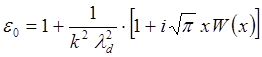
где , , .

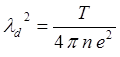Приближение холодной плазмы получится при , . Воспользуемся выписанным ранее разложением W(x) для случая , удержав первые три члена в мнимой части

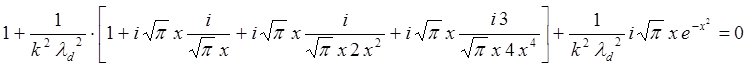      (5.3.25)

Так будет выглядеть дисперсионное соотношение в принятом нами приближении. Преобразуем его

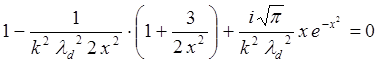                                            (5.3.26)

и далее

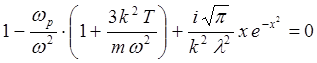                  (5.3.26а)

Определим теперь действительную и мнимую части частоты. Действительную часть найдем из соотношения

                                                         (5.3.27)

что означает в нашем случае

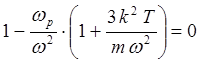                                           (5.3.28)

И в случае, когда , т.е. при рассмотрении нами ленгмюровских колебаний, дает окончательно

                                              (5.3.29)

Из сказанного вытекает ограничение на длину волны ленгмюровских колебаний

                                                              (5.3.30)

означающее, что упомянутая длина волны должна быть больше дебаевского радиуса плазмы.

Найдем далее мнимую добавку к частоте

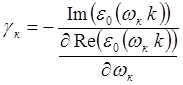                                            (5.3.31)

Из выражения (5.3.26)

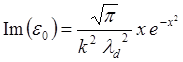                                             (5.3.32)

и учетом того, что

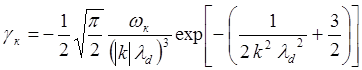            (5.3.33)

Отрицательная мнимая добавка к частоте означает, что колебания затухают. Такое бесстолкновительное затухание называется затуханием Ландау. Из формулы (5.3.33) видно, что для ленгмюровских колебаний это затухание становиться экспоненциально малым при  (тогда отрицательный показатель экспоненты  и ). Если же , то влияние экспоненты ограничено и затухание весьма существенно. Поэтому ленгмюровские колебания с длиной волны меньше дебаевского радиуса являются сильно затухающими.

5.3.4  .Раскачка волн пучком частиц.

Рассмотрим систему, состоящую из электронного пучка, проходящего сквозь плазму. Будем интересоваться достаточно высокочастотными колебаниями, чтобы ионную компоненту можно было исключить из рассмотрения. Исходим из общего выражения для диэлектрической проницаемости(5.3.24):