Взаимодействие частиц в плазме. Кулоновские столкновения

Глава 4.         Взаимодействие частиц в плазме.

4.1.Основные понятия теории столкновений.

            Процесс взаимодействия частиц называется столкновением в том случае, если он происходит за отрезок времени, гораздо более короткий, чем все другие, интересующие нас процессы, и мы не рассматриваем развитие его во времени, а интересуемся только исходным и результирующим состоянием системы. Обычно принимаются в расчет только парные столкновения – во-первых они наиболее вероятны, а во-вторых изучение , скажем, тройного столкновения, вызывает серьезные математические трудности. Считается, что столкновение произошло, если частицы вначале сближались друг с другом, а потом разошлись, причем произошло какое-то физическое изменение в этой системе.

            Столкновение называется упругим, если в результате этого столкновения происходит изменение лишь энергии и импульса взаимодействующих частиц. Упругие столкновения приводят к рассеянию, торможению пучков частиц; к охлаждению более горячей и нагреву более холодной компонент плазмы

            Столкновение называется неупругим, если в результате этого столкновения происходит изменение внутренней энергии частиц или рождение новых (исчезновение исходных) частиц. Неупругие столкновения соотносятся с процессами возбуждения, ионизации, диссоциации и обратных им изменений состояния взаимодействующих частиц.

Для описания столкновений применяется вероятностный подход.

Вероятность того или иного результата столкновения определяется так называемым эффективным сечением столкновения. Обычно его обозначают греческой буквой s.

Эффективное сечение столкновения s может рассматриваться как величина, пропорциональная обратной средней длине свободного пробега. В приближении, при котором взаимодействующие частицы моделируются непроницаемыми упругими шариками, средняя длина свободного пробега в однородном газе дается формулой, выведенной Максвеллом:

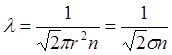                                                (4.1.1.)

Здесь n – число атомов или молекул в 1см³ , r – радиус шарика, моделирующего рассматриваемую частицу. Величина s =pr² , введенная здесь, имеет смысл площади поперечного сечения цилиндра, «заметаемого» модельным шариком. Всякий другой шарик, попадающий полностью или частично внутрь этого цилиндра, испытает столкновения с «пробным» шариком. Если рассматривать шарики двух сортов (1 и 2), имеющие разные радиусы (r₁  и r₂), то нетрудно показать, что средняя длина свободного пробега частиц сорта 1 в среде частиц сорта 2 выразится формулой

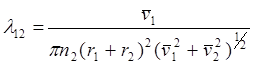                              (4.1.2.)

Полное число таких столкновений в 1 секунду

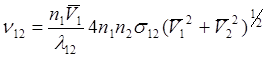                             (4.1.3)

Здесь  ; .

При столкновениях электронов с атомами газа (частицы сорта 1 – электроны, частицы сорта 2 – атомы) и . При этом (4.1.2.) и (4.1.3) будут выглядеть соответственно:

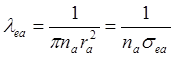                                           (4.1.2.а)

                                                   (4.1.3а)

            Наряду с моделью упругих непроницаемых сфер, применяются и другие модели; главным отличием их друг от друга является форма пространственного распределения потенциала взаимодействия и классичность или квантовость подхода к рассмотрению процесса столкновения.

4.2.Кулоновские столкновения.

Поскольку важнейшим признаком плазмы, является определяющая роль

 кулоновского характера взаимодействия частиц, нам следует обратить особое внимание на кулоновские столкновения.

4.2.1.   Кулоновский логарифм и особенности кулоновского взаимодействия.

Изучение характеристик этого взаимодействия удобно начать с модельной задачи по расчету силы, действующей на неподвижный «кулоновский центр» со стороны «налетающего» на него плоского потока заряженных частиц.

Пусть имеется точечный заряд  q_a  , помещенный в точке пространства, принимаемой нами за начало отсчета и закрепленный там неподвижно. Из бесконечности вдоль оси z на него налетает однородный плоский поток частиц с массой m и зарядом q_b.  Требуется найти усредненную силу, действующую на этот неподвижный заряд со стороны налетающего потока.

·   

· 

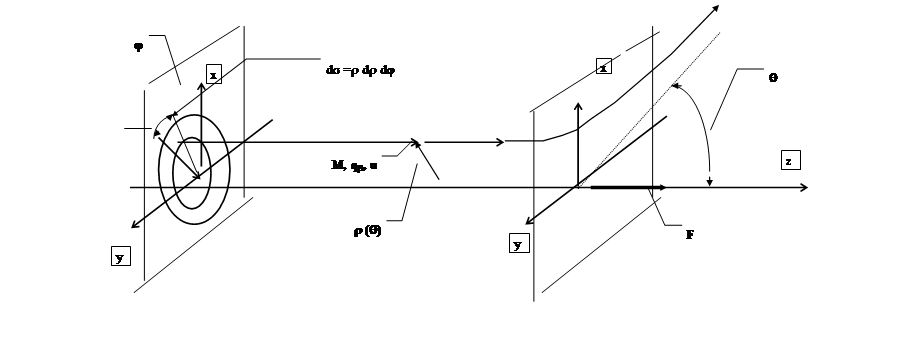
Рис. 4.1.

Рассмотрение будем вести в приближении парных соударений, то - есть будем считать, что в каждый момент с кулоновским центром взаимодействует только одна частица. Решение задачи о рассеянии одной заряженной частицы на неподвижном кулоновском центре хорошо известно еще со времен Резерфорда поэтому мы воспользуемся этим результатом. Рассеиваемая частица движется по гиперболе и угол рассеяния q связан с прицельным параметром  r соотношением:

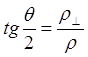                                                                    (4.2.1)

где  r_^ = (q_a q_b )/mU²- значение прицельного параметра, при котором частица отклоняется на прямой угол   q = p /2 .Сечение  рассеяния вычисляется по формуле Резерфорда.

Результирующая сила, действующая на рассеивающий центр со стороны потока частиц направлена вдоль оси z в связи с однородностью этого потока. По величине она равна силе, действующей в обратном направлении - со стороны рассеивающего центра на поток. Вычислить ее можно, зная изменение суммарного импульса частиц потока в единицу времени

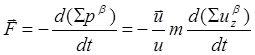                                  (4.2.2)

Поскольку столкновения считаем упругими, скорость налетающих частиц не меняется по величине :  u^’ = u

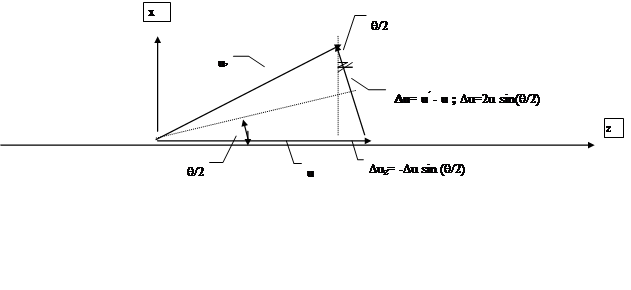Рис.4.2.

Изменение проекции каждой частицы на ось z  будет в результате выглядеть следующим образом :

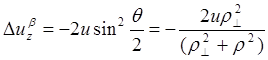                              (4.2.3)

Здесь использована связь q и r , даваемая уравнением  (3.2.1).