Взаимодействие частиц в плазме. Кулоновские столкновения, страница 2

Через элементарную площадку  ds =r dr dj за единицу времени проходит число частиц потока  n_b u ds . Умножив эту величину на изменение импульса одной частицы  Dp_z^b =m Du_z^b  и интегрируя по всей плоскости, найдем суммарное изменение импульса потока частиц в единицу времени и, следовательно, силуF :

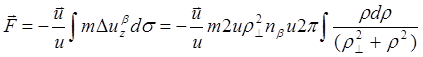             (4.2.4)

Интеграл, входящий в выражение (  4)  логарифмически расходится при  r ® µ , что дает физически неприемлемый результат. Чтобы получить конечное значение для силы Fверхний предел интегрирования необходимо ограничить некоторым значением r_max  >> r_^ . Тогда, обозначив получающееся значение интеграла через  L, получим :

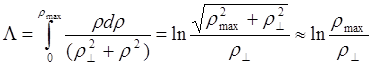               (4.2.5)

Подставив затем в формулы (4.2.4) и (4.2.5) значение r_^ = (q_a q_b )/mU² , имеем

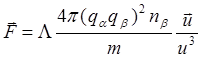                                    (4.2.6)

где 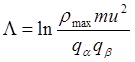                                                                   (4.2.7)

так называемый  «кулоновский логарифм»; его значение зависит от выбора верхнего предела интегрирования по r . В условиях плазмы за  r_max логично выбрать величину дебаевского радиуса, так как именно эта величина является характерным пространственным масштабом , определяющим расстояние, на котором происходит резкое ослабление поля точечного заряда.

Таким образом в плазменных условиях имеем следующее выражение для кулоновского логарифма :

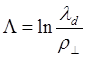                                                   (4.2.8)

В теории плазмы принято разделение на «близкие» и «далекие» пролеты при кулоновских взаимодействиях. Близкие пролеты дают рассеяние на большие углы, далекие - на малые. Условной границей между близкими и далекими  пролетами выбрано значение прицельного параметра   r_min  = 2 r_^ . Интеграл в формуле (4.2.5) может быть в связи с этим разбит на две части:

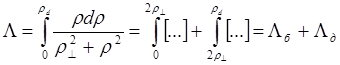                 (4.2.9)

 

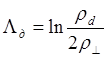
Поскольку сила, действующая на кулоновский центр, находящийся в потоке частиц, пропорциональна кулоновскому логарифму, то разделение его на две части делит на две составляющие и эту силу. При этом вклад далеких пролетов оказывается определяющим :

4.2.2.   Сила трения при кулоновском рассеянии частиц.

Определим теперь среднюю силу, действующую на заряженную частицу с массой m _a , зарядом q _a , движущуюся со скоростью v через среду, состоящую из частиц с массой m_b  и  зарядом q_b , распределенных по скоростям в соответствии с некоторой функцией распределения

По-прежнему считаем соударения парными. Выпишем уравнения движения для пары взаимодействующих частиц :

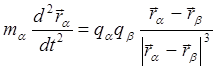
(4.2.10)

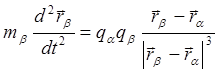m _b

Удобнее перейти к рассмотрению движения центра инерции нашей механической системы, состоящей из двух частиц  и относительного движения этих частиц. Введем радиус-вектор центра инерции :

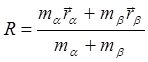                                                      (4.2.11)

и вектор относительного расстояния между взаимодействующими частицами :

                                                                                                             (4.2.12)

Тогда радиус-векторы положения частиц можно выразить через эти новые переменные :

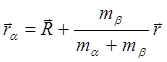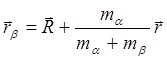  ;                         (3.2.13)

и, подставив в  (4.2.10) , получим уравнение движения центра инерции :

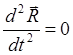                                                         (4.2.14)

и уравнение относительного движения частиц :

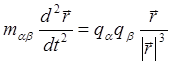                                     (4.2.15)

где    

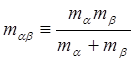
Из  (4.2.14)  следует :  , что соответствует состоянию равномерного прямолинейного движения или покоя (без ограничения общности рассмотрения можем положить ). Уравнение  (4.2.15) напоминает любое из исходных уравнений движения частиц (4.2.10) и описывает движение некоторой частицы с массой m _{a b}  в поле неподвижного кулоновского центра, что дает нам возможность использовать результат предыдущего параграфа.

Напомним, что нас интересует сила, действующая на пробную частицу a. Вернемся поэтому к выражению для ее радиус-вектора (первое из выражений (4.2.13). Умножим его на массу m _a и дважды продифференцируем по времени :

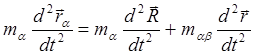                                (4.2.16)

С учетом уравнения (4.2.14) это превратится в следующее соотношение :

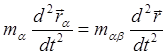                                                  (4.2.17)

означающее, что сила, действующая на частицу в единичном  столкновении совпадает с силой как бы действующей на фиктивную частицу с приведенной массой, налетающей на воображаемый неподвижный центр. Этот неподвижный центр, как уже отмечалось в предыдущем параграфе, подвергается действию противоположно направленной силы той же величины.

Теперь мы должны построить промежуточную модель плоского потока рассеиваемых частиц. Выделим из всех частиц среды только частицы, имеющие скорость v^’ . Плотность частиц такого элементарного потока:

                                     (4.2.18)

Заметим еще, что  фиктивные частицы с «приведенной» массой налетают на воображаемый неподвижный рассеивающий центр со скоростью :

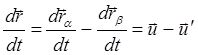                                (4.2.19)

Теперь нам остается лишь заменить переменные в выражении  (3.2.6) предыдущего параграфа в соответствии со следующей схемой :

; ;                      (4.2.20)

чтобы получить силу, действующую со стороны выделенного элементарного потока частиц на неподвижный центр :

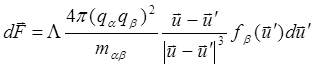                                (4.2.21)

Изменив знак силы на противоположный и интегрируя по всем скоростям, получаем:

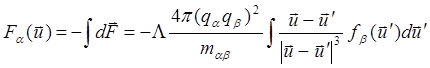                     (4.2.22)

причем в данном случае в кулоновский логарифм входит некая усредненная величина  < r_^> :

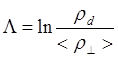                                                (4.2.23)

где

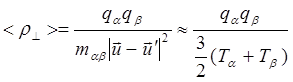(3.2.24)

Анализ выражения  (4.2.22) дает, в частности, такой очень важный результат : сила трения при кулоновском рассеянии обратно пропорциональна квадрату модуля скорости