Excel, решение численных задач, линейных и нелинейных уравнений

Ниже мы рассмотрим решение средствами Excel некоторых популярных задач вычислительной математики, которые имеют как самостоятельное, так и прикладное значение.

11.1. Решение уравнений

11.1.1. Решение нелинейных уравнений

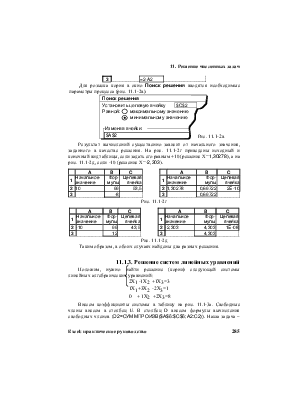
Положим, нужно найти корень квадратного уравнения вида 0,5X2-3X+4=0. Решение будем искать в клетке А1, куда занесем исходное значение корня, например 0. Само уравнение внесем в А2. На рис. 11.1-1а изображены эти клетки в числовой форме, на рис. 11.1-1б – в виде формул. На рис. 11.1-1в изображен результат вычислений с помощью подбора параметра

    Рис. 11.1-1а            Рис. 11.1-1б            Рис. 11.1-1в

Исходные значения параметров, участвующих в вычислениях, изображены на рис. 11.1-1г в окне Подбор параметра.

Точный корень нашего уравнения, как мы знаем, равен 2. Полученный результат очень близок, но не равен 2. Это естественно, поскольку Excel использует не аналитические (как мы привыкли), а численные, итерационные методы, заключающиеся в постепенном приближении получаемого решения к точному. Критерием сходимости процесса считается близость очередного и предшествующего значений подбираемых решений. По умолчанию Excel выполняет до 1000 итераций или продолжает вычисления до достижения погрешности, не превышающей 0,0001. Если вы хотите изменить эти значения, следует в меню Сервис+Пара­метры во вкладке Вычисления осуществить необходимые установки.