Excel, логарифмические, тригонометрические и обратные тригонометрические функции

Упражнения

Логарифмические функции

Логарифмические функции вычисляют натуральные и общие логарифмы чисел. LN(x) и EXP(x) вычисляют натуральный логарифм x и число e, возведённое в степень x (x – показатель степени числа e - e^x) соответственно. Теоретически значение x в экспоненциальной функции может принимать любое значение; однако значение x более 709,782 приводит к численному переполнению, и в этом случае функция возвращает ошибочное значение #ЧИСЛО!.

Функция EXP(1) возвращает основание e натурального логарифма (2,71828182845905). LOG10(x) возвращает десятичный логарифм (основание 10) x. LOG(x;b) возвращает логарифм x по любому основанию b.

№ 36. Вычислить:

а) log₂64;                       ж) log₃2 * log₄3 * log₅4 * log₆5 * log₇6 * log₈7;

б) log₅(1/25);                  з) log₂7;

в) log_1/28;                        и) lg 56;

г) lg10;                           к) log₉₈28;

д) ln(1/e);                       л)

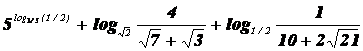
е) lg2;

№ 37. Сравнить (что больше): log_0,52 + log_0,57 и log_0,5(2+7)

Тригонометрические функции

Тригонометрические функции SIN(x), COS(x) и TAN(x) возвращают синус, косинус и тангенс угла x соответственно. Угол x должен быть в радианах, поэтому следует преобразовать показатель величины угла в градусах в показатель в радианах, для чего можно воспользоваться функцией РАДИАНЫ( ), либо сделать это путём умножения на p/180. Например, если y выражен в градусах, формула для получения синуса y будет следующей:

SIN(РАДИАНЫ(Y)) = SIN(Y*ПИ( )/180).

Для обратного процесса и преобразования показателя угла в радианах в градусы воспользуйтесь функцией ГРАДУСЫ( ) или умножьте на 180/p. Вот, например, формула для получения арксинуса z в градусах: