С целью проверки результатов можно вычислить определенный интеграл вручную
![]() 1 1
1 1
S = òХ2dx = Х3/3 = 1/3=0,333.
0 0
Видим, что результат, полученный методом трапеций, уже весьма близок к точному.
11.3. Решение дифференциальных уравнений
Дифференциальные уравнения являются основной формой представления математических моделей. Напомним, что уравнение, в котором неизвестная функция входит под знаком производной или дифференциала, называется дифференциальным уравнением. Если неизвестная функция, входящая в дифференциальное уравнение, зависит только от одной независимой переменной, то уравнение называется обыкновенным. Обыкновенное дифференциальное уравнение в общем случае содержит независимую переменную (X), неизвестную функцию (Y(X)) и ее производные (dY/dX) до n-го порядка и имеет вид
F(X, Y, Y¢, Y², ... , Y(n))=0.
Порядком дифференциального уравнения называется наивысший порядок производной, входящей в уравнение.
Здесь мы рассмотрим технику решения обыкновенных дифференциальных уравнений с начальными условиями, т.е. таких, для которых известны значения искомой функции и ее производных (до n-1 порядка) при Х=0. Решение уравнений в такой постановке называется задачей Коши.
Известно, что аналитическое решение дифференциальных уравнений возможно лишь в небольшом числе случаев. В остальных случаях оно доступно только с помощью численных методов. Самый простой из них – метод Эйлера. Суть метода применительно к дифференциальному уравнению первого порядка dY/dX=Y(X,Y) с начальными условиями Y(X0)=Y0 поясняет рис. 11.3а.
|
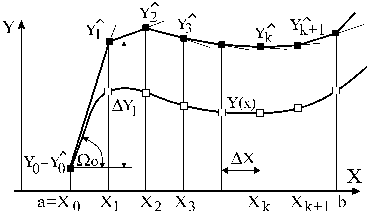
Решением уравнения является такая функция Y(Х), которая, будучи подставленной в уравнение, превращает его в тождество. Само уравнение не известно. В начальных условиях задается только одна его точка Y(Х0). Разобьем весь диапазон интегрирования уравнения на участки с одинаковым шагом DХ и попытаемся найти значение искомой функции Y(Х) в точке Х1=Х0+DХ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.