Excel, решение численных задач, линейных и нелинейных уравнений, страница 2

Нами получено одно из решений квадратного уравнения. Другое вещественное решение (если есть) возможно будет найдено, если задать иное начальное значение Х.

11.1.2. Решение систем нелинейных уравнений

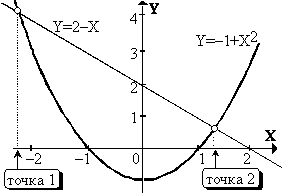
Положим, имеется система двух нелинейных уравнений:

                                               Y=2-X

                                                Y=-1+X2,

которые надо решить, т.е. найти точки их пересечения. Как видно на рис. 11.1-2а, такая система имеет две точки пересечения.

Для решения системы построим таблицу (рис. 11.1-2б), где в клетки В2 и В3 введем обе функции, которые в качестве аргумента Х ссылаются на ячейку А2. Кроме того, для контроля вычислений в С2 вводится целевая функция, которая вычисляет среднее отклонение значений функций друг от друга. Очевидно, если эти функции пересекаются (т.е. имеются решения), С2=0.