











|
Министерство профессионального и общего образования РФ Новосибирский государственный технический университет Кафедра техники и электрофизики высоких напряжений |
|
|
|
Расчетное задание на тему: |
|
Основы математической статистики |
|
Выполнил |
|
студент группы Эн1-52 Вариант№ Принял: |
|
Савинов А. А. 94 Кандаков С. А. |
|
Новосибирск 2007 |
|
Вариант задания №94: |
|
|
|
|
|
|
|
|
|
|
|
|
|
Цель расчетного задания: |
|
Ознакомление с основными задачами, решаемыми методами математической статистики: - определением оценок числовых характеристик случайных величин и их систем; - оценкой точности и надежности этих характеристик; - проветкой прадоподобия различных гипотез: об объединяемости двух выборок; о подчинении данного статистического материала некоторому закону распределения; о наличии или отсутствии корреляционной связи между случайными величинами; - определением коэффициентов линейной регрессии случайных величин X и Y и оценкой ее статистической значимости. Статистической обработке подвергаются две выборки случайных величин X и Y. |
|
Решение |
|
1) |
|
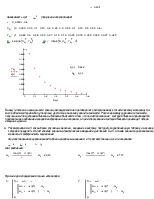
Определить оценки мат. ожидания и дисперсии случайных величин X и Y, заданных в виде двух простых статистических совокупностей. |
|
Статистические оценки математического ожидания и дисперсии генеральных совокупностей X и Y, удовлетворяющие требованиям состоятельности, несмещенности и эффективности: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2) |
|
Проверить правдоподобие гипотезы о принадлежности двух выборок X и Y единой генеральной совокупности с помощью трех критериев и определить уровни значимости, с которыми проверяемая гипотеза не противоречит располагаемому статистическому материалу. |
|
a) Порядковый критерий Вилькоксона : Для использования порядкового критерия Вилькоксона необходимо составить единый вариационный ряд для двух выборок X и Y(перемешанный по признаку возрастания элементов выборок). Критерием согласия выдвинутой гипотезы о принадлежности двух выборок единой генеральной совокупности служат числа инверсий, характеризующие степень перемешанности единого вариационного ряда. |
|
Составление единого вариационного ряда: |
|
|
|
|
|
|
|
Сортировка ряда по признаку возрастания элементов: |
|
|
|
|
|
Функция для вычисления числа инверсий: |
|
|
|
В случае, когда в выборках X и Y присутствуют равные элементы первым всегда берется элемент выборки, матрица которой стоит в функции на первом месте. |
|
Число инверсий иксов с игреками: |
|
|
|
|
|
Число инверсий игреков с иксами можно вычислить по формуле: |
|
|
|
|
|
|
|
- так как для вычисления уровня значимости необходимо большее из двух чисел |
|
Числа инверсий подчинены нормальному закону с параметрами: |
|
|
|
|
|
|
|
|
|
Поскольку порядковый критерий Вилькоксона является двусторонним критерием, уровень значимости определится по формуле(с учетом приведенных выше равенств): |
|
|
|
- функция Лапласа |
|
|
|
|
|
|
|
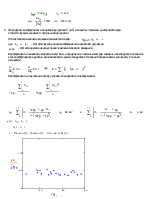
b) Критерий равенства математических ожиданий: |
|
В случае, когда исследователь располагает только объемами выборок и статистическими оценками их математических ожиданий и дисперсий, для оценки правдоподобия гипотезы о принадлежности двух выборок единой генеральной совокупности можно воспользоваться критерием равенства математических ожиданий двух независимых выборок - критерием Z: |
|
|
|
|
|
Случайная величина Z при справедливости выдвинутой гипотезы распределена по нормальному закону с параметрами |
|
|
|
|
|
Следовательно, так как критерий Z двусторонний, уровень значимости выдвинутой гипотезы о принадлежности двух выборок единой генеральной совокупности при наблюденном значении критерия Z определится как: |
|
|
|
|
|
c) Критерий равенства дисперсий (Р. Фишера): |
|
При использовании критерия равенства дисперсий двух независимых выборок задача заключается в проверке, является ли значимым различие в оценках дисперсий выборок X и Y (В этом случае в качестве критерия проверки используется статистика Р. Фишера): |
|
|
|
|
|
- так как в качестве числителя берут большую из оценок дисперсий. |
|
F - распределение зависит тоько от чисел степеней свободы: |
|
|
|
|
|
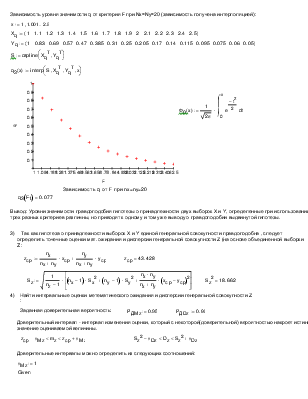
Зависимость уровня значимости q от критерия F при Nx=Ny=20 (зависимость получена интерполяцией): |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.