Определение числовых характеристик отдельных выборок. Критерий Вилькоксона и проверка гипотезы об однородности двух выборок. Сравнение двух дисперсий нормальных генеральных совокупностей (критерий Фишера)

Министерство образования Российской Федерации                         НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ  УНИВЕРСИТЕТ 

Кафедра  тепловых электрических станций

Контрольная работа

по дисциплине: « Теория вероятности и математической статистики »

Группа: ЭТз-81

 Шифр:340758107                                                                                                                                                                               

Студент: Малютин.М.Ю.

Преподаватель:

Новосибирск 2010

                             1.Математическая статистика

В результате измерения случайной величины Х получены две выборки объемами n₁ и n₂. По данным выборкам Х₁ и Х₂ выполнить следующее:

1.  Определить точечные оценки числовых характеристик (математического ожидания и дисперсии) для каждой выборки Х₁ и Х₂ в отдельности и для объединенной выборки.

2.  Проверить правдоподобие гипотезы о принадлежности двух выборок Х₁ и Х₂ единой генеральной совокупности с помощью порядкового критерия Вилькоксона, критериев равенства математических ожиданий (Z - статистика, Т – статистика Стьюдента) и дисперсий двух выборок (критерий Фишера).

3.  Построить гистограмму и эмпирическую функцию распределения для единой генеральной совокупности.

4.  Определить доверительные интервалы числовых характеристик математического ожидания и дисперсии для каждой выборки Х₁ и Х₂ в отдельности.

5.  Определить доверительные интервалы числовых характеристик (математического ожидания и дисперсии) для каждой выборки Х₁ и Х₂ в отдельности, с помощью точных методов.

6.  Проверить гипотезу о нормальном законе распределения генеральной совокупности Х по критерию Пирсона.

7.  Определить оценку коэффициента корреляции между двумя случайными величинами Х₁ и Х₂.

8.  Проверить гипотезу об отсутствии корреляционной связи между двумя случайными величинами Х₁ и Х₂.

    Дано:

Выборка X₁

9,68	9,27	7,87	9,42	8,55
8,75	10,78	11,41	8,02	10,20
10,23	9,16	11,54	8,15	9,34
9,48	11,01	9,11	10,50	10,64

Выборка X₂

11,69	10,32	12,79	9,11	10,89
9,92	8,21	11,19	10,70	8,89
10,77	10,58	9,15	10,25	9,07
10,64	10,81	7,92	11,10	9,01

Определение числовых характеристик отдельных выборок

Статистические оценки математического ожидания и дисперсии генеральной совокупности Х, удовлетворяющие требованиям состоятельности, несмещенности и эффективности, определяются по выражениям:

                         

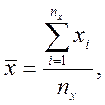
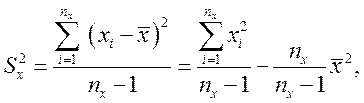
где  - оценка математического ожидания генеральной совокупности Х;

 - оценка дисперсии генеральной совокупности Х;

n_x  –  объем выборки из генеральной совокупности Х.

Оценки числовых характеристик для объединенной статистической выборки Х определяются на основе вычисленных значений  для выборок Х₁ и  Х₂ по выражениям:

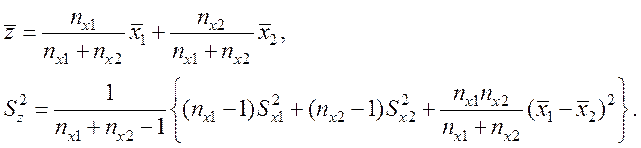
         Решение:

Для выборок Х₁ и Х₂, распределения которые приведены выше, необходимо определить оценку математического ожидания и оценку дисперсии генеральной средней совокупности.

Оценка математического ожидания выборки Х₁:

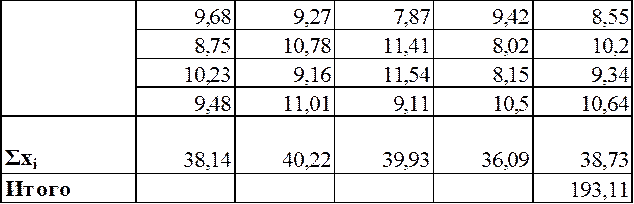
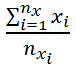==  = 9,656

Оценка дисперсии выборки Х₁:

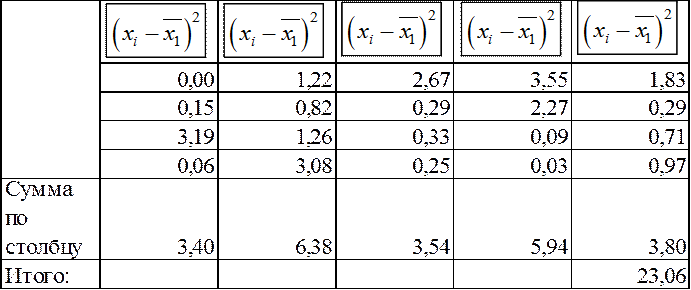
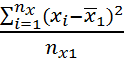=  =  = 1,21

Оценка математического ожидания выборки Х₂:

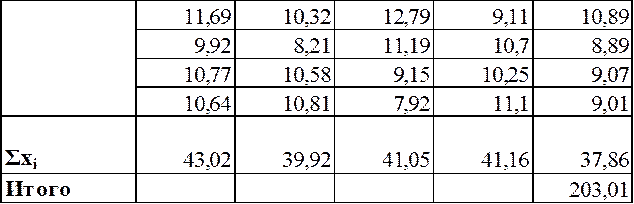
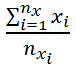==  = 10,15

Оценка дисперсии выборки Х₂:

	2,37	0,03	6,97	1,08	0,55
	0,05	3,76	1,08	0,3	1,58
	0,38	0,18	1	0,01	1,17
	0,24	0,44	4,97	0,9	1,3
Сумма по столбцу:	3,04	4,41	14,02	2,29	4,6
Итого:					28,36

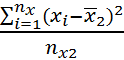=  =  = 1,49

Оценка математического ожидания для объединенной выборки X₁ и Х₂:

 =  9,656 +  10,15 = 4,83 + 5,08 = 9,91

=  {(20-1)1,21 + (20-1)1,49 +  (9,656 – 10,15)² }= 53.74

2.Критерий Вилькоксона и проверка гипотезы об
однородности двух выборок.

Критерий Вилькоксона служит для проверки однородности двух независимых выборок: x₁, x₂, …, x_n; y₁, y₂, …, y_n. Достоинство этого критерия состоит в том, что он применим к случайным величинам, распределения которых неизвестны, требуется лишь, чтобы величины были непрерывны.

Если выборки однородны, то считают, что они извлечены из одной и той же генеральной совокупности и следовательно имеют одинаковые, причем неизвестные, непрерывные функции распределения F₁(x), F₂(x).

Нулевая гипотеза состоит в том, что при всех значениях аргумента (х) функции распределения равны между собой: F₁(x) = F₂(x).

Проверка нулевой гипотезы в случае, если объем обеих выборок не превосходит 25.