Рассмотрим случай параллельного соединения, для элемента А1 (рис. 2№1). Вероятность прохождения электрического сигнала по цепи, определяется из того, чтобы либо элемент R1, либо R2, либо оба вместе были в работоспособном состоянии, т.е. применима теорема сложения для совместных событий:
P(![]() ) =
P(
) =
P(![]() ) +
P(
) +
P(![]() ) -
P(
) -
P(![]() );
);
P(![]() ) =
0,8+0,8 – 0,8·0,8 = 0,96.
) =
0,8+0,8 – 0,8·0,8 = 0,96.
Гораздо проще данную задачу решить через противоположные события, если предположить, что элементы неработоспособны. Тогда, вероятность того, что электрический сигнал не пройдет, определяется из того, что и элемент R1, и элемент R2 будут неработоспособны, т.е. применяется теорема умножения:
P(![]() ) = P(
) = P(![]() )· P(
)· P(![]() );
);
P(![]() ) = 0,2 · 0,2 =
0.04
) = 0,2 · 0,2 =
0.04
Чтобы определить вероятность прохождения сигнала, т.е. противоположное событие, необходимо:
P(![]() ) = 1- P(
) = 1- P(![]() ) · P(
) · P(![]() );
);
P(![]() ) = 1 – 0,04 =
0,96
) = 1 – 0,04 =
0,96
Два разных подхода дают одинаковые результаты.
Определим вероятность прохождения сигнала по элементу А2 (рис 2 №2).
Рассмотрим случай последовательного соединения. Сигнал пройдет по цепи, если оба элемента R1 и R2 будут работоспособны, с вероятностью 0,8, т.е. применима теорема умножения независимых событий:
P(![]() ) =
P(
) =
P(![]() ) ·
P(
) ·
P(![]() );
);
P(![]() ) =
0.8 · 0.8 = 0,64
) =
0.8 · 0.8 = 0,64
Если последовательно имеется n элементов, то применимо следующее выражение:
![]()
Определим вероятность прохождения по элементу А2
P(![]() ) = P(
) = P(![]() ) · P(
) · P(![]() );
);
P(![]() ) = 0,96 · 0,64
= 0,614;
) = 0,96 · 0,64
= 0,614;
Вероятность прохождения сигнала по элементу А4 (рис 2 №4):
P(![]() ) =[[
P(
) =[[
P(![]() ) · P(
) · P(![]() )+ P(
)+ P(![]() )]- [
P(
)]- [
P(![]() ) ·
P(
) ·
P(![]() )· P(
)· P(![]() )]]· P(
)]]· P(![]() ) =
) =
[[0.8·0.8 + 0.8]- [0.8·0.8·0.8]]·0.8 = 0,742.
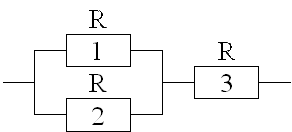
Определим вероятность прохождения по элементу А3
P(![]() ) =
[1- P(
) =
[1- P(![]() )· P(
)· P(![]() )]· P(
)]· P(![]() ) ;
) ;
P(![]() ) =
[1 – 0,2·0,2]·0,8 = 0.768.
) =
[1 – 0,2·0,2]·0,8 = 0.768.
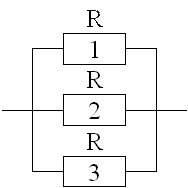
Определим вероятность прохождения по элементу А5
P(![]() ) = 1
- P(
) = 1
- P(![]() )· P(
)· P(![]() )· P(
)· P(![]() ) ;
) ;
P(![]() ) =
1- 0,2·0,2·0,2 = 0,992.
) =
1- 0,2·0,2·0,2 = 0,992.
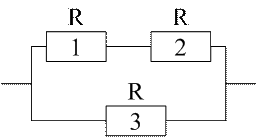
Определим вероятность прохождения по элементу А6
P(![]() ) = [P(
) = [P(![]() ) · P(
) · P(![]() )+ P(
)+ P(![]() )]- [
P(
)]- [
P(![]() ) ·
P(
) ·
P(![]() )· P(
)· P(![]() )];
)];
P(![]() ) = [0,8·0,8+0,8]-[0,8·0,8·0,8]
= 0,928.
) = [0,8·0,8+0,8]-[0,8·0,8·0,8]
= 0,928.
Так как элемент В неизвестен, но известно, что это может быть с одинаковой вероятностью элементы А3или А5, илиА6 т.е. данные схемы равновероятны, следовательно, можно найти вероятность прохождения электрического сигнала, как средневзвешенную сумму вероятностей для элементов А3 и А5 и А6
P(B)
= 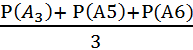 ;
;
P(B) = ![]() =
0,896.
=
0,896.
В заключении, подставляем все найденные вероятности элементов цепи Е:
P(E)
= P(![]() )· P(
)· P(![]() )·P(B)·
P(
)·P(B)·
P(![]() );
);
P(E) = 0,96·0,614·0,896·0,742 = 0,3919.
Таким
образом, вероятность прохождения сигнала по цепи Е равно 39,19%. ![]()
 A6
A6
A5
6.Математическое ожидание и дисперсия. Мода и медиана. Моменты.
Задание.
При заданной плотности распределения непрерывной случайной величины найти ее математическое ожидание, дисперсию, среднеквадратическое отклонение, моду и медиану.
|
Номер варианта |
|
||
|
7 |
|
Решение.
· Математическое ожидание:
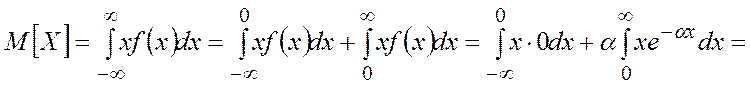
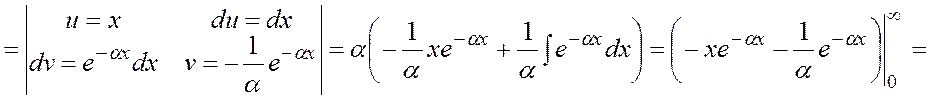
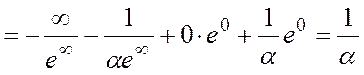
· Дисперсия:
![]()
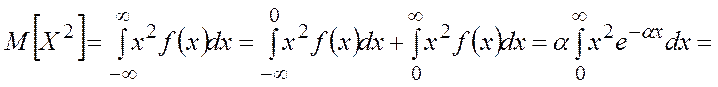
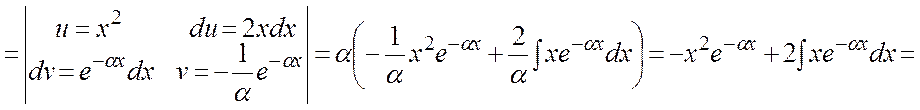
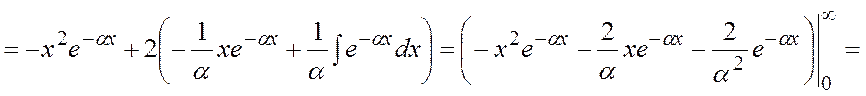
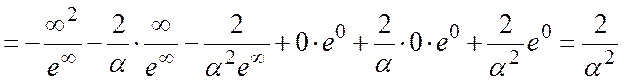
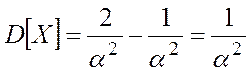
· Среднеквадратическое отклонение:
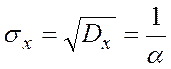
· Мода.
Для того чтобы найти моду, определим максимум плотности распределения:
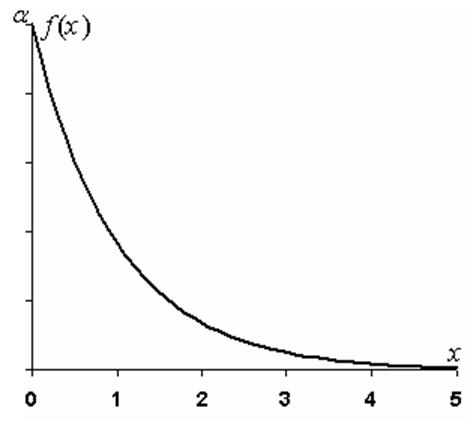
Максимальное
значение ![]() функция плотности распределения принимает
при
функция плотности распределения принимает
при ![]() , значит
, значит ![]() .
.
· Медиана.
Для определения медианы решим следующее уравнение:
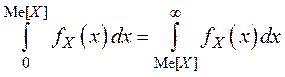
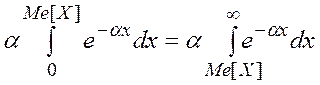
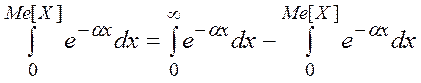
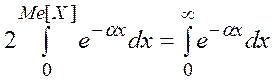
Проинтегрируем по отдельности левую и правую части:
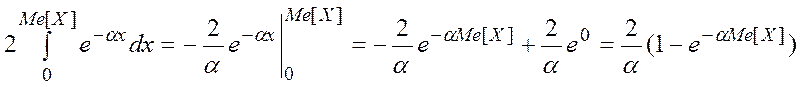
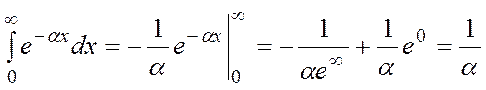
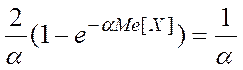
![]()
![]()
![]()
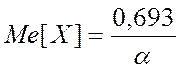
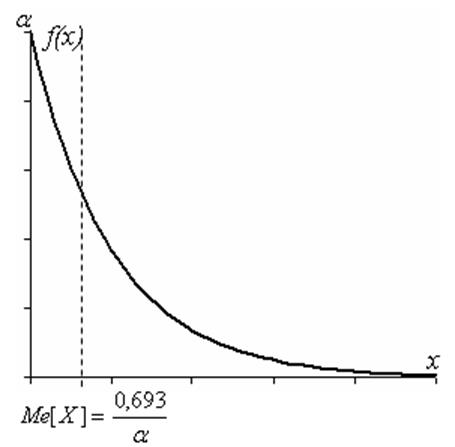
Таким образом, при заданной плотности распределения непрерывной случайной величины Х, ее числовые характеристики будут равны:
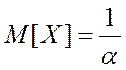
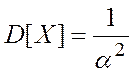
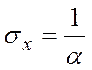
![]()
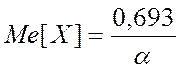
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.