Математика \ Теория вероятностей и математическая статистика

Определение числовых характеристик отдельных выборок. Критерий Вилькоксона и проверка гипотезы об однородности двух выборок. Сравнение двух дисперсий нормальных генеральных совокупностей (критерий Фишера), страница 4

Интервал, I

Количество значений, ni приходящиеся на интервал I

Частота наблюдений,

pi = ni/n

7,5-8,0

1

8,0-8,5

2

8,5-9,0

2

9,0-9,5

6

9,5-10,0

1

10,0-10,5

3

10,5-11,0

2

11,0-11,5

2

    11,5-12,0

1

∑ = 20

∑ = 1

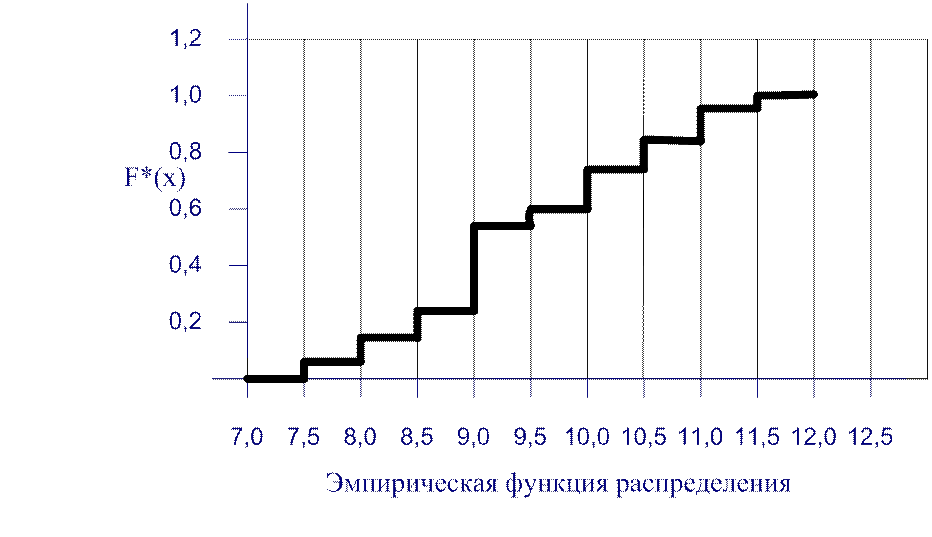
Наименьшая варианта Х равна 7,5, значение меньше 7,5 не наблюдалось, следовательно, F*(x) = 0. Значение Х < 8,0 наблюдалось 1 раз, F*(x)=1/20 = 0,05,при 7,5 < x ≤ 8,0. Следующее значение равно 8,5, x<8,5, а именно х1 = 7,5 и х2 = 8,0, наблюдалось 1+2 = 3 раза, F*(x) = 3/20 = 0,15, при 8,0<x≤8,5.

Иначе можно суммировать частоты наблюдений pi, т.е. при 8,0<x≤8,5, F*(x) = p1+p2 = 0,05 + 0,1 = 0,15, и.т.д.

Искомая эмпирическая функция распределения имеет вид:

                                                   0.при х;

                                                0,05, при 7,5<x8,0;

F*(x)=   {                   0,15, при  8,0<x;

                                     0,25 ,при 8,5<x9,0    (0,05+0,1+0,1=0,25);

                               0,55,при 9,0<x9,5   (0,05+0,1+0,1+0,3=0,55);

                             0,6,при 9,5<x10,0  (0,05+0,1+0,1+0,3+0,05=0,6);

                            0,75,при 10,0<x10,5 (0,05+0,1+0,1+0,3+0,05+0,15=0,75);

                                                 0,85,при 10,5<x11,0

                                                  0,95,при 11,0<x11,5

                                              1,при 11,5<x12,0

5. Доверительный интервал и доверительная вероятность для математического ожидания.

В ряде задач требуется найти не только некоторый параметр распределения - x, но и оценить его точность и надежность. Требуется знать, к каким ошибкам может привести замена параметра х, его точечной оценкой  и с какой степенью уверенности можно ожидать, что эти ошибки не выйдут за определенные пределы?

Чтобы дать представление о точности и надежности оценки , в статистике используют доверительный интервал и доверительную вероятность.

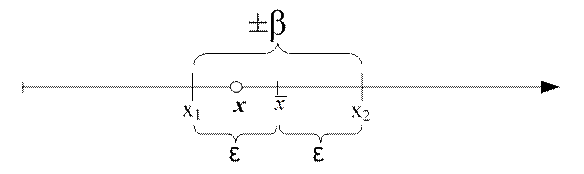
Пусть для параметра х получена из опыта несмещенная оценка , необходимо определить ошибку. Для этого назначим некоторую большую вероятность β (0,9; 0,95; 0,99), такую, что с вероятностью β можно считать практически достоверным:

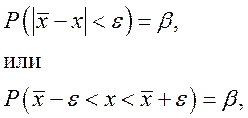
 что означает, что с вероятностью β неизвестное значение, х попадает в интервал:

. Вероятность β называется доверительная вероятность, а интервал Iβ – доверительный интервал, границы интервала – доверительные границы.

Решение:

Определим доверительный интервал для исходной задачи (таблица 1, выборка Х1). Оценка математического ожидания, равна 9,656 , выборочная дисперсия 1,21.

Примем доверительную вероятность β=0,8, тогда

ε = 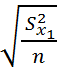 arg Ф 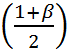 = 0,25 arg Ф(0,9) = 0,25 · 1,29 = 0,32,

где arg Ф(0.9) определяется по таблице приложения 1. При Ф(0.9), х=1,29.

Доверительные границы: m1 = -3.67 = 9,656 – 0,32=9,336,

 m2  =+3,67= 10,15 + 0,32 = 10,47. Таким образом, истинное значение математического ожидания случайной величины подчиненной нормальному закону распределения находится в интервале (9,336;10,47).

Доверительный интервал и доверительная вероятность для дисперсии.

          Аналогичным образом может быть построен доверительный интервал для дисперсии.

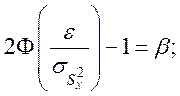
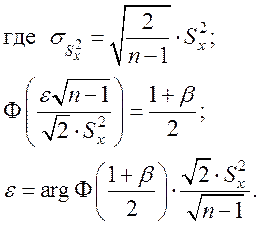
          Тогда, доверительный интервал для дисперсии определиться так:

.

Решение:

Определим доверительный интервал для дисперсии (таблица 1, выборка Х1). Оценка математического ожидания, равна 9,656, выборочная дисперсия 1,21.

Примем доверительную вероятность β=0,8, тогда

ε = 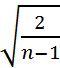 arg Ф 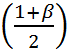= 0,392 arg Ф(0,9) =0,392 · 1,29 = 0,506

Доверительные границы: D1 = -0,506 = 0,704, D2  =+0,506=1,716. Таким образом, истинное значение математического ожидания случайной величины подчиненной нормальному закону распределения находится в интервале (0,704;1,716).

Точные методы построения доверительных интервалов для параметров случайных величин, распределенных по нормальному закону.

Определение точных доверительных интервалов
для оценки математического ожидания.

Для точного нахождения доверительных интервалов совершенно необходимо знать заранее вид закона распределения величины Х, тогда как для применения приближенных методов это не обязательно.

Скачать файл