Определение числовых характеристик отдельных выборок. Критерий Вилькоксона и проверка гипотезы об однородности двух выборок. Сравнение двух дисперсий нормальных генеральных совокупностей (критерий Фишера), страница 5

Закон распределения оценки х в общем случае зависит от самих неизвестных параметров величины Х. Однако удается перейти в неравенствах от случайной величины х к какой – либо другой функции наблюденных значений, закон распределения которых не зависит от неизвестных параметров, а зависит только от числа опытов n и от вида закона распределения. При нормальном распределении величины Х случайная величина Т,

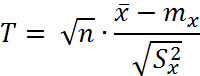
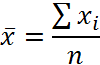
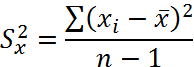
Подчиняется закону распределения Стьюдента, с n-1 степенями свободы.

Доверительный интервал для оценки математического ожидания:

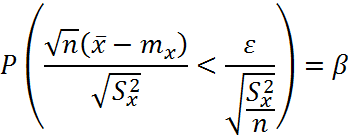
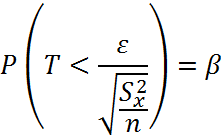
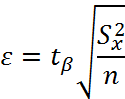
Значение t_β определяется по таблице приложения 2. Тогда, доверительный интервал:

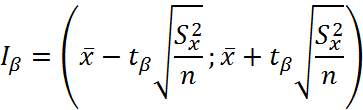
Решение:

 Определим доверительный интервал для оценки математического ожидания – 9,656, S_x² = 1,21, n=20, β = 0,8.

Определяем t_β(β,n-1)=t_β(0.8;19)=1,3277 (по таблице приложения 2). Далее определяем величину ошибки

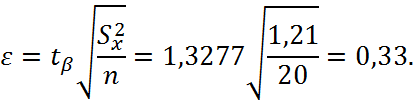
Тогда значения доверительного интервала лежат в пределах:

I_β=(9,656-0,33; 9,656+0,33) = (9,326; 9,986). Иными словами, истинное математическое ожидание случайной величины Х, распределенной по нормальному закону распределения, лежит в интервале от 9,326 до 9,986, с точностью 80%.

Надо отметить, что полученные доверительные интервалы с помощью точных методов мало отличаются от значений доверительных интервалов, полученных приближенным способом: I_β=(9,336; 10,47) – для приближенного метода.

Определение точных доверительных интервалов для оценки дисперсии.

Оценка дисперсии: 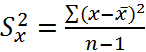. Случайная величина 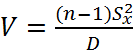 имеет распределение χ² (так называемое «хи квадрат» распределение с n-1 степенями свободы). Выразим несмещенную оценку дисперсии через случайную величину V:

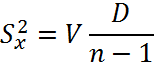
Зная закон распределения величины V, можно определить интервал I_β, в который она попадает с заданной вероятностью β.

Закон распределения величины Vс n-1 степенями свободы несимметричен относительно математического ожидания, поэтому, вероятность выхода величины V за пределы интервала вправо и влево должны быть одинаковы: .

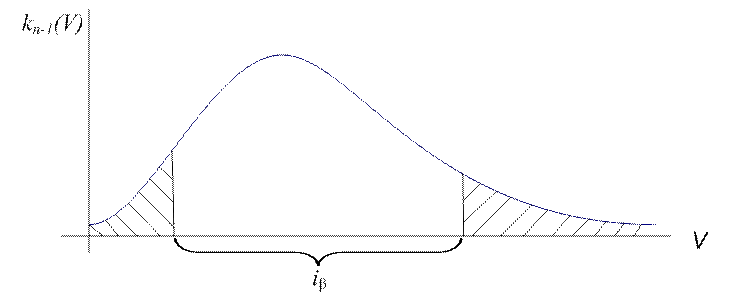
χ²=p₁=, χ²=p₂ = 1-. Значения χ² берутся из таблицы 4 приложения [Вентцель Е. С., Теория вероятностей].

В итоге получаем доверительный интервал, который накрывает точку D (истинное значение дисперсии) с вероятностью β:

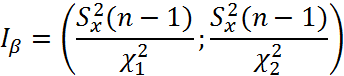
Решение:

Определим доверительный интервал для оценки дисперсии, если известно, но величина Х распределена нормально.

Исходные данные:

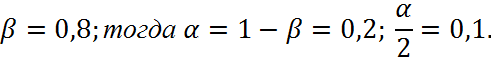
Определяем левую и правую вероятность, распределения по таблице 4:

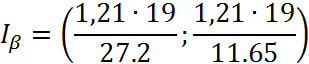
Доверительный интервал  накрывает истинную оценку дисперсии. Если сравнивать полученный интервал с доверительным интервалом по приближенному методу, то видны существенные расхождения в значениях.

6.Тема: Основные понятия теории вероятностей.

ЗАДАНИЕ.

Электрическая цепь Е состоит из четырех элементов множества А={А₁, А₂, …, А₁₀}. Каждый из элементов этого множества выполнен из элементов типа R по различным схемам. Элемент В цепи точно неизвестен. Однако известно, что с одинаковой вероятностью это может быть элемент А₃, или А₅, или А₆. Определить вероятность прохождения электрического сигнала по цепи n-m, если вероятность выхода из строя каждого элемента типа R равна 0.2.

№ варианта	Е	1	2	3	4
7	3	1	4	В	10

                               Таб.1 Варианты электрической цепи Е.

                          №3

             

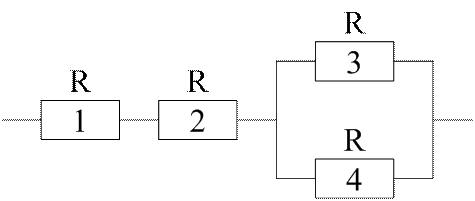
                                  Рис.1  Электрическая цепь Е.

    №1

                                         

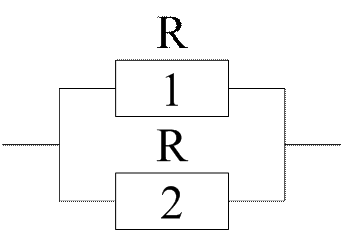
                   №2

                           

                                 №4

                                             

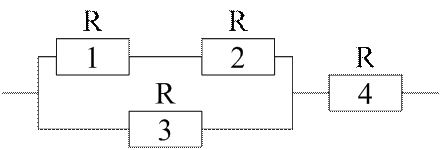
  Рис. 2. Элементы цепи Е.

         Решение:

Электрическая цепь Е (рис. 1) состоит из четырех элементов множества А={А₁, А₂, …, А₄}. Каждый из элементов этого множества выполнен из элементов типа R по различным схемам (рис. 2). Элемент В (номер 3 на рис 1.) цепи точно неизвестен. Однако известно, что с одинаковой вероятностью это может быть элемент А₃, или А₅ ,или А₆. Определить вероятность прохождения электрического сигнала по цепи n-m, если вероятность выхода из строя каждого элемента типа R равна 0,2.

Первоначально определим вероятности прохождения сигнала по каждому из элементов А₁ - А₅ в отдельности.