Правило 1. Для того чтобы при заданном уровне значимости a = 2Q проверить нулевую гипотезу Н0: F1(x) = F2(x) об однородности двух независимых выборок объемов n1 и n2 (n1≤n2) при конкурирующей гипотезе H1: F1(x) ≠ F2(x), надо:
1. расположить варианты обеих выборок в возрастающем порядке, т.е. в виде одного вариационного ряда, и найти в этом ряду наблюдаемое значение критерия Wнабл – сумму порядковых номеров вариант первой выборки;
2. найти по таблице приложения 4 нижнюю критическую точку wнижн.кр (Q; n1,n2), где Q=a/2;
3. найти верхнюю критическую точку по формуле
wверх.кр = (n1 + n2 +1)·n1 - wнижн.кр. (1)
Если Wнабл < wнижн.кр или Wнабл > wверх.кр - нулевую гипотезу отвергают.
Если wнижн.кр < Wнабл < wверх.кр – нет оснований отвергнуть нулевую гипотезу.
Проверка нулевой гипотезы в случае, если объем, хотя бы одной из выборок превосходит 25.
Правило 2. При конкурирующей гипотезе F1(x) ≠F2(x) нижняя критическая точка определяется следующим образом:
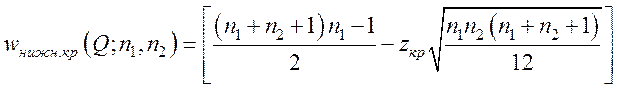 ,
,
где
Q = α/2; zкр находят по таблице функции Лапласа (приложение 1) с
помощью равенства 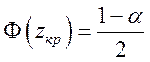 . В остальном правило 1 остается
без изменений.
. В остальном правило 1 остается
без изменений.
Решение:
Даны две выборки Х1 и Х2. Определить, однородны ли две выборки?
Примем уровень значимости a =0,01. Пусть нулевая гипотеза заключается в равенстве функций распределений F1(x) = F2(x), конкурирующая гипотеза F1(x) ≠ F2(x)
Расположим варианты обеих выборок в виде одного вариационного ряда и перенумеруем их:
|
Порядковые номера |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
Варианты |
7,87 |
7,92 |
8,02 |
8,15 |
8,21 |
8,55 |
8,75 |
8,89 |
9,01 |
9,07 |
9,11 |
|
Порядковые номера |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
|
Варианты |
9,11 |
9,15 |
9,16 |
9,27 |
9,34 |
9,42 |
9,48 |
9,68 |
9,92 |
10,20 |
10,23 |
|
Порядковые номера |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
31 |
32 |
33 |
|
Варианты |
10,25 |
10,32 |
10,50 |
10,58 |
10,64 |
10,64 |
10,70 |
10,77 |
10,78 |
10,81 |
10,89 |
|
Порядковые номера |
34 |
35 |
36 |
37 |
38 |
39 |
40 |
||||
|
Варианты |
11,01 |
11,10 |
11,19 |
11,41 |
11,54 |
11,69 |
12,79 |
Примечание: полужирным начертанием обозначены варианты первой
выборки, курсивом обозначены варианты соответственно второй выборки.
Найдем наблюдаемое значение критерия Вилкоксона – сумму порядковых номеров вариант первой выборки:
Wнабл = 2+3+4+6+7+12+14+15+16+17+18+19+21+22+25+27+31+34+37+38+41 = 409.
Найдем по таблице 10 нижнюю критическую точку, учитывая, что
Q = a/2 = 0,01/2 = 0,005, ![]() = 0.375(по
таблице функции Лапласа)
= 0.375(по
таблице функции Лапласа)
n1 = n2 = 20: wнижн.кр = 375,4.
По формуле (1), определим верхнюю критическую точку:
wверх.кр = (20+20+1)·20-375,4 = 444,6.
Так как, 375,4<409<444,6 , следовательно wнижн.кр < Wнабл < wверх.кр, и нет оснований опровергать нулевую гипотезу об однородности двух выборок.
Критерии равенства математических ожиданий и дисперсий
1. Сравнение двух средних генеральных совокупностей, дисперсии которых известны (большие независимые выборки)
Допустим,
имеются две большие независимые выборки объемом n и m (n>30, m>30), по
которым найдены соответствующие выборочные средние - ![]() и
известны генеральные дисперсии
и
известны генеральные дисперсии![]() .
.
Для того чтобы при заданном уровне значимости α проверить нулевую гипотезу H0: M(X1)=M(X2) о равенстве математических ожиданий (генеральных средних) двух нормальных генеральных совокупностей с известными дисперсиями (в случае больших выборок) при конкурирующей гипотезе H1: M(X1)≠M(X2), надо вычислить наблюдаемое значение критерия
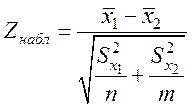 ,
,
и по таблице Лапласа (приложение 1) найти критическую точку zкр из равенства
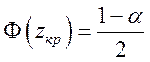 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.