Оценка параметров распределения методом моментов и методом максимального правдоподобия. Проверка гипотезы о нормальности выборки по критерию хи-квадрат

Задание:

Выборка из нормального распределения:

1.80     1.85     1.90     0.38     0.41     2.32     1.00     1.07

2.39     -0.66   2.31     0.52     3.23     0.32     -0.82   1.82

0.61     0.11     1.42     1.97     -0.21   2.48     2.20     1.54

0.70     1.49     1.60     -0.12   1.11     0.20     1.95

1)  Найти оценки параметров распределения методом моментов и методом максимального правдоподобия.

Оценка методом моментов:

Поскольку математическое ожидание - выборочный момент первого порядка, т.е. среднее значение х, с одной стороны, и – неизвестный параметр распределения a, с другой, то

Второй выборочный момент равен:

Поскольку    , то параметр  можно вычислить следующим образом:

 

Оценка методом максимального правдоподобия:

Плотность нормального распределения равна:

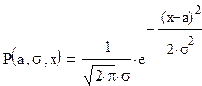
                                                                                         (1.1)

Составим функцию правдоподобия как произведение n членов вида (1.1):

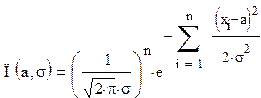
Прологарифмировав данное выражение, получим логарифмическую функцию правдоподобия:

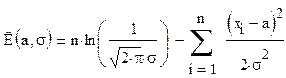
                                                                       (1.2)

Продифференцировав (1.2) по а и приравняв нулю, получаем, что

Продифференцировав (1.2) по  и приравняв нулю, получаем, что

Подставив значения выборки в выражения для расчетов параметров распределения, имеем

2)  Подставить вместо неизвестных параметров их оценки. Записать выражение для оценки плотности распределения.

Подставив вместо неизвестных параметров их оценки, получим выражение для оценки плотности распределения:

 

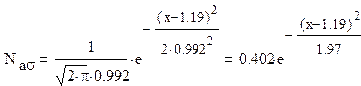
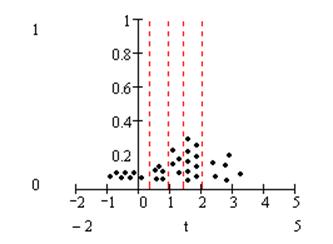
3)  Построить на одном графике гистограмму с шагом равным СКО и график оценки плотности распределения.

Количество столбцов гистограммы равно:

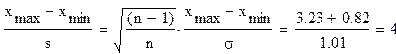
4) Проверить гипотезу о нормальности выборки по критерию хи-квадрат. Для этого разбить числовую ось на интервалы равной вероятности (основываясь на оценках параметров выборки). Число интервалов выбрать по формуле Стёджеса. Оценить достигаемый уровень значимости и сделать вывод о принятии гипотезы:

а) на уровне 0.1;

б) на уровне 0.01;

в) на уровне 0.001;

Рассчитаем число промежутков по формуле Стёджеса:

Взяв целую часть log2(n), получим:

Отсюда вероятность попадения хi  в промежуток равной вероятности равна:

Расчет длин интервалов равной вероятностей произведем по формуле функции Лапласа

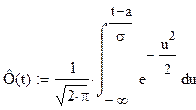
Отсюда интервалы равной вероятности:

Расчет произведем по формуле:

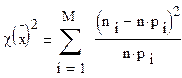
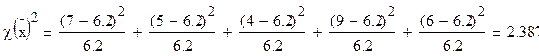
Воспользуемся таблицей оценки по критерию хи-квадрат:

Число степеней свободы вычисляется по формуле М-s-1, где М-число интервалов равной вероятности (в нашем случае М=5), s-число неизвестных параметров (в нашем случае s=2), то есть число степеней свободы равно 2.

М-s-1	0,1	0,01	0,001
2	4,61	7,24	9,21

Вывод: Гипотеза принимается на уровнях 0,1; 0,01; 0,001.