В режиме
максимальной мощности естественно положить ![]() , где
, где ![]() —
максимально допустимый ток смещения диода, a
—
максимально допустимый ток смещения диода, a ![]() . Это позволяет получить соотношения для расчета выходной
мощности
. Это позволяет получить соотношения для расчета выходной
мощности ![]() генератора,
мощности
генератора,
мощности ![]() , потребляемой от источника смещения, мощности
, потребляемой от источника смещения, мощности ![]() рассеяния на диоде, КПД генератора, эквивалентной проводимости
диода по первой гармонике
рассеяния на диоде, КПД генератора, эквивалентной проводимости
диода по первой гармонике ![]() и его
индуктивности
и его
индуктивности ![]() :
:
![]() ;
;
![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
; ![]() .
.
Индуктивность лавины
![]() , где
, где ![]() —
характеристическое время процесса лавинообразования с учетом влияния объемного
заряда;
—
характеристическое время процесса лавинообразования с учетом влияния объемного
заряда; ![]() — время
пролета электронов через область дрейфа;
— время
пролета электронов через область дрейфа; ![]() — средняя скорость дрейфа электронов.
— средняя скорость дрейфа электронов.
Пролетная частота
![]()
Емкости
лавинной ![]() и пролетной
и пролетной
![]() областей
определяем из соотношения
областей
определяем из соотношения
![]() , где
, где ![]() — площадь сечения диода;
— площадь сечения диода; ![]() — электрическая проницаемость полупроводника. Обычно
— электрическая проницаемость полупроводника. Обычно ![]() , т.е.
, т.е. ![]() .
.
Условием
существования стационарного режима работы генератора на ЛПД так же, как для
диодов Ганна, является равенство эквивалентной проводимости диода по первой
гармонике ![]() эквивалентной
проводимости
эквивалентной
проводимости ![]() параллельного колебательного контура, подключенного к
диоду:
параллельного колебательного контура, подключенного к
диоду:
![]() ;
;
![]() ;
;
![]()
Приведенные выше соотношения используют для расчета колебательной системы автономного генератора. Расчет энергетических характеристик обычно дает несколько завышенные результаты, так как при их выводе не учитывались свойства диода и размыв лавины при прохождений носителями области пролета. Кроме того, при работе ЛПД в режиме большого сигнала в такт с полным напряжением иизменяется ширина обедннёной области и увеличивается объемный заряд в пролетном пространстве диода.
12.6. Анализ режимов работы автогенератора с использованием годографа
Анализ
стационарного режима АГ. Для анализа
стационарного режима АГ удобно использовать годографы выходной проводимости ![]() активного
элемента и проводимости
активного
элемента и проводимости ![]() колебательной системы.
колебательной системы.
Годограф
проводимости ![]() — это линия на комплексной плоскости
— это линия на комплексной плоскости ![]() . по которой перемещается конец радиус-вектора
. по которой перемещается конец радиус-вектора ![]() при
изменении аргумента от 0 до ∞ [8, 18]. Направление годографа соответствует
возрастанию аргумента. Аргумент
при
изменении аргумента от 0 до ∞ [8, 18]. Направление годографа соответствует
возрастанию аргумента. Аргумент ![]() — частота ω, аргумент
— частота ω, аргумент ![]() — амплитуда колебаний
— амплитуда колебаний ![]() - Варианты годографов показаны на рис. 12.23.
- Варианты годографов показаны на рис. 12.23.
Точка
пересечения годографов ![]() и
и ![]() определяет
стационарный режим колебаний. Так как каждая точка годографа
определяет
стационарный режим колебаний. Так как каждая точка годографа ![]() соответствует определенной частоте, а годографа
соответствует определенной частоте, а годографа ![]() —определенной амплитуде колебаний, то пересечение
—определенной амплитуде колебаний, то пересечение ![]() с
с ![]() позволяет найти частоту
позволяет найти частоту ![]() и амплитуду
колебаний в стационарном режиме
и амплитуду
колебаний в стационарном режиме ![]()
Для построения годографов необходимо знать зависимости:
•
![]() или
или![]() и
и ![]() , которые находятся методами расчета линейных цепей;
, которые находятся методами расчета линейных цепей;
•
![]() или
или ![]() и
и ![]() , которые
находятся расчетом режима A3 при разных амплитудах
, которые
находятся расчетом режима A3 при разных амплитудах ![]() (определение
(определение
![]() , фазового
сдвига φмежду
, фазового
сдвига φмежду ![]() и
и ![]() как функции
как функции
![]() ,а
затем составляющих
,а
затем составляющих ![]() :
: ![]() и
и![]() )
)
 |
 В случае, если мнимая часть проводимости
В случае, если мнимая часть проводимости 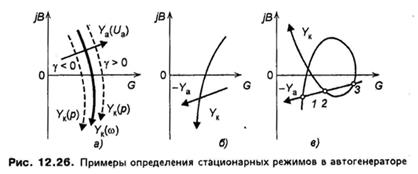 Анализ устойчивости стационарного режима автоколебаний. Анализ устойчивости стационарных режимов удобно
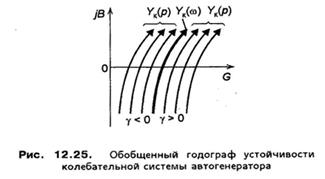
проводить с помощью обобщенного годографа проводимости
Анализ устойчивости стационарного режима автоколебаний. Анализ устойчивости стационарных режимов удобно
проводить с помощью обобщенного годографа проводимости ![]() , под
которым понимается совокупность линий на комплексной плоскости
, под
которым понимается совокупность линий на комплексной плоскости ![]() , по которым перемещается радиус-вектор
, по которым перемещается радиус-вектор ![]() при
изменении комплексной частоты
при
изменении комплексной частоты ![]() ,
, ![]() . В
этом случае процесс изменения амплитуды
. В
этом случае процесс изменения амплитуды ![]() в
переходном процессе записывается в виде
в
переходном процессе записывается в виде ![]() .
Обобщенный годограф
.
Обобщенный годограф ![]() показан на
рис. 12.25. Обобщенный годограф связан с годографом
показан на
рис. 12.25. Обобщенный годограф связан с годографом ![]() , имеет такую же форму и расположен
справа от него, если
, имеет такую же форму и расположен
справа от него, если ![]() , и слева,
если
, и слева,
если ![]() (если
смотреть по направлению возрастания частоты).
(если
смотреть по направлению возрастания частоты).
На рис.
12.26 показаны варианты графического решения уравнения ![]() ,
определяющего стационарные режимы колебаний.
,
определяющего стационарные режимы колебаний.
• Рис. 12.26,а. Полагаем, что ![]() уменьшилось, т.е. рабочая точка сместилась по
годографу влево, попала на годограф
уменьшилось, т.е. рабочая точка сместилась по
годографу влево, попала на годограф ![]() при
при ![]() . Так как
. Так как ![]() , то при
уменьшении амплитуды колебаний возникает переходной процесс, стремящийся
увеличить
, то при
уменьшении амплитуды колебаний возникает переходной процесс, стремящийся
увеличить ![]() и восстановить стационарный режим.
и восстановить стационарный режим.
• Рис. 12.26,6. Стационарный режим неустойчив.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.