Выбор схем радиопередатчиков и определение их основных параметров. Расчет усилителей мощности. Расчет умножителей частоты. Расчет модуляторов, страница 20

                                                                  (11.3)

Вычислим максимально возможную мощность в нагрузке УЧ с учетом допустимых параметров транзистора: напряжения на коллекторе *, тока коллектора , напряжения на эмиттере и мощности рассеяния . При расчете будем предполагать, что транзистор находится в критическом режиме. С теми же допущениями, что и в усилителях, будем считать границей насыщения линию, проходящую через начало координат выходных характеристик с наклоном .

*В качестве величины, ограничивающей напряжение на коллекторе, взято смещение Е_к, а не напряжение пробоя , а поскольку УЧ, как правило, не оконечный каскад передатчика, то величина Е_к определяется из расчета оконечного каскада или задана для всего передатчика.

Если ограничено , то максимальная мощность, создаваемая генератором тока с учетом настройки выходной цепи в резонанс, , , где . Отсюда . В дальнейшем величину  будем использовать в качестве нормирующей.

Чтобы рассчитать мощность в нагрузке , надо учесть распределение тока генератора между  и  (см. рис. 11.2). В рассматриваемом режиме коэффициент распределения тока

                                                                                          (11.4)

Где , в активной области. Можно показать, что значения А при  практически постоянны. С учетом  мощность в нагрузке

                                                                         (11.5)

Отсюда максимальная мощность . Отметим, что эту мощность нельзя реализовать, поскольку из-за малых  (здесь  )приходится работать с большим , а следовательно, с большим импульсом тока , который обычно больше допустимого . Величина  может быть ограничена предельно допустимым током коллектора  или предельно допустимым напряжением на эмиттерном переходе: . Исходя из последнего условия, определим допустимый ток . Ток , где  — максимальное напряжение на эмиттерном переходе в активной области. Учитывая, что в области отсечки  не должно превышать величину , получаем

.                                                                       (11.6)

Итак, если при расчете максимальной мощности исходить из допустимого тока, то .

Теперь рассчитаем мощность Р_н в критическом режиме при условии, что ограничены одновременно напряжение () и ток ():

 .                                                                                                        (11.7)

На первый взгляд, выражение (11.7) при и   должно определять максимальную мощность в нагрузке. Покажем, что это действительно так, но при одном условии. Предположим, что ограничения по отсутствуют, и введем в (11.7) безразмерный импульс тока Z = i_KM/(S_KE_K) = 1 - .   Тогда

 .                                                                                           (11.8)

Отсюда максимальная мощность получается при

Z = 2А/(1 + 2А)   ( = 0,5),                                                                                            (11.9)

т.е. в режиме согласования

.                                                                                       (11.10)

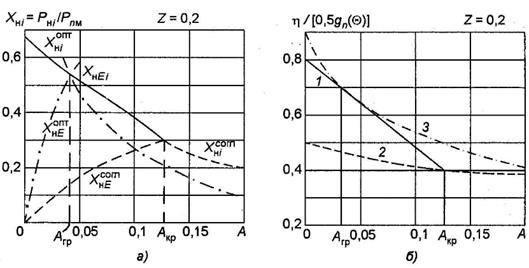
Рис. 11.3. Зависимости нормированных мощностей (а) и КПД (б) от параметра А в режимах: максимального использования по напряжению и току (1); согласования (2) и оптимального КПД (3)

Эта мощность может быть реализована, если требуемое напряжение меньше допустимого: , т.е. . Подставив в последнее неравенство из (11.9), находим критическое значение : . При переходе через это значение максимальная мощность (рассчитываемая при  по (11.7) получается в режиме согласования и определяется по (11.10). Отметим, что проведенный расчет подобен расчету мощности в нагрузке лампового генератора, выполненного по сложной схеме. Параметр эквивалентен в этом случае КПД промежуточного контура.

Режим согласования может быть реализован не только при работе с допустимым током, но и при Е_к = Е_{к доп}. Для расчета мощности в (11.5) надо подставить Е_к = Е_{к лоп} и величину , определенную из условия :

.                                                                                    (11.11)