2. ПОЛИНОМИАЛЬНЫЕ МАТРИЦЫ
В этом разделе рассмотрим взаимно простые полиномы, взаимно простые полиномиальные матрицы и представление полиномиальных матриц через взаимно простые разложения. Взаимная простота в матричном случае в некотором смысле эквивалентна наблюдаемости и управляемости динамических систем.
2.1. Взаимно простые полиномы. Матрица Сильвестра
Пусть d(s) будет полиномом с вещественными коэффициентами и переменной s: d(s)= dnsn+dn-1sn-1+…+d1s+d0. Полином d(s) называют полином степени (degree) n1 если dn≠0. Коэффициент dn, соответствующий старшей степени s, называют ведущим коэффициентом (leading coefficient). Полином называют нормированным (monic), если его ведущий коэффициент равен единице.
Теорема 2.1. Пусть d(s) и n(s) два полинома и пусть d(s) ≠ 0. Тогда существуют единственные полиномы q(s) и r(s) такие, что
n(s)=q(s)d(s)+r(s), deg r(s)< degd(s).
Определение 2.1. Полином r(s) является наибольшим общим делителем (greatest common divisor) d(s) и n(s), если r(s) является общим делителем d(s) и n(s), и делится на каждый общий делитель d(s) и n(s). Если наибольший общий делитель d(s) и n(s) есть нулевая константа, то d(s) и n(s) называю относительно простыми или взаимно простыми (relatively prime или comprime).
Теорема 2.2. Любой наибольший общий делитель полиномов d(s) и n(s) может быть выражен в форме
r(s)=x(s)d(s)+y(s)n(s), где x(s) и y(s) полиномы.
Теорема 2.3. Рассмотрим два полинома d(s) ≠ 0 и n(s).Тогда d(s) и n(s) взаимно простые, если и только если имеет место одно из условий:
1.
Для каждого s из
ℂ матрица 2*1 ![]() имеет
ранг 1.
имеет
ранг 1.
2. Существуют два полинома x(s) и y(s) такие, что
x(s)d(s)+y(s)n(s)=1.
3. Но существуют полиномы a(s) и b(s), таких что
n(s)/d(s)=b(s)/a(s)
или эквивалентно
 (2.1)
(2.1)
и deg a(s )< deg d(s).
Определение 2.2. Матрицей Сильвестра (Sylvester matrix) или результатом (resultant) для двух полиномов
d(s) = d0 + d1s + … + dnsn, n(s) = n0 + n1s +…+ nmsm.
где dn ≠ 0, nm ≠ 0, называется квадратная матрица размером n+m
s≜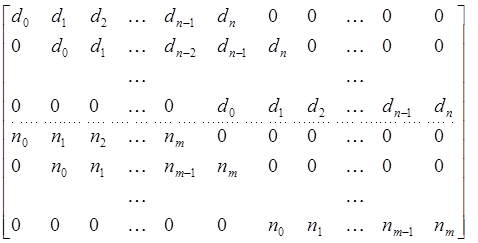
Решение уравнения (2.1) состоит в следующем. Пусть
d(s) = d0 + d1s + … + dnsn, ( dn ≠ 0); (2.2)
n(s) = n0 + n1s + …+ nmsm , (nm ≠ 0); (2.3)
и пусть
a(s)=a0+a1s+…+an-1sn-1; (2.4)
b(s)=b0+b1s+…+bm-1sm-1. (2.5)
По (2.2) – (2.5) составляется матрица Сильвестра. Справедливо.
Следствие 2.1. Полиномы d(s) и n(s) взаимно простые, если и только если матрица Сильвестра несингулярная.
Пусть заданы два полинома
d(s) = d0 + d1s + … + dnsn,
n(s) = n0 + n1s + …+ nnsn,
где dn ≠ 0. Пусть два полинома a(s) и b(s) определены так:
a(s)=a0+a1s+…+aкsк;
b(s)=b0+b1s+…+bкsк.
По уравнению –b(s)d(s)+a(s)n(s)=0 можем составить матричное уравнение
![]() , (2.6)
, (2.6)
где матрица sk размерами 2(k+1)*(n+k+1):
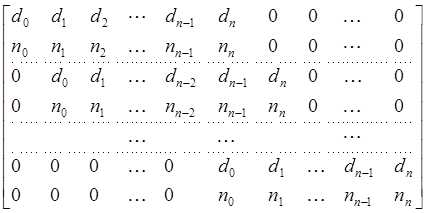 (2.7)
(2.7)
Теорема 2.4. Рассмотрим два полинома d(s) и n(s) со степенями degn(s )<degd(s)= n. a(s) и b(s), вычисленные по (2.4) посредством использования первых линейно зависимых строк матрицы sк, оказываются взаимно простыми.
Следствие 2.2. Два полинома d(s) и n(s) со степенями degn(s ) < degd(s) = n взаимно простые, если и только если квадратная матрица sк-1 порядка 2n несингулярная или если и только если общее число линейно независимых n –строк в sn-1 равно n.
Пример 2.1. Рассмотрим полиномы d(s) = -2s4+ 2s3-s2- s+1 и n(s)=s3+2s2-2s+3. Формируем результат:
 . (2.8)
. (2.8)
Для поиска линейно зависимых строк S используем строчный поисковой алгоритм. Ведущие элементы выделены рамочками. Результат следующий:
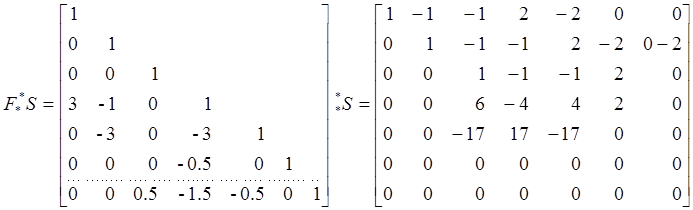 ≜
≜![]() .
.
В матрице ![]() пять
ненулевых строк, следовательно, результат S имеет ранг
пять и вырожден. Таким образом, для первой нулевой строки
пять
ненулевых строк, следовательно, результат S имеет ранг
пять и вырожден. Таким образом, для первой нулевой строки ![]() мы можем получить из первых шести строк F
посредством рекурсивной формулы (1.9), уравнение
мы можем получить из первых шести строк F
посредством рекурсивной формулы (1.9), уравнение
![]() .
.
Используя (2.4), (2.5) и (2.6), получаем:
a(s) = s2 -0.5, b(s) = -0.5s -1.5
и n(s)/d(s) = b(s)/a(s) = (s+3)/(-2s2 + 1)
Здесь d(s) и n(s) взаимно простые полиномы.
2.2. Взаимно простые полиномиальные матрицы
Матрицу с полиномиальными элементами называют полиномиальной матрицей (polynomial matrix). Аналогично матрицам с элементами из ℝ или ℂ мы можем ввести следующие элементарные операции над A(s):
1.Умножение строки или столбца на ненулевое вещественное или комплексное число.
2.Перестоновка любых двух строк или столбцов.
3.Добавление произведения строки или столбца на полином к другой строке или столбцу.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.