Функциональное моделирование привода. Синтез системы управления приводом. Функциональная модель электропривода. Виртуальная модель электропривода

1. Задание.

Получить результаты функционального моделирования привода:

- под заданный график изменения нагрузки с целью уточнения эквивалентных значений моментов и токов по «гладкой составляющей»;

- под выбранные вид и параметры настройки регулятора в различных режимах работы в разомкнутой и замкнутой системах;

Все решения в пояснительной записке должны быть иллюстрированы блок-диаграммами, временными диаграммами и выводами.

2. Параметры выбранного двигателя.

Момент нагрузки – реактивный. М_наг = 0,45 Н*м.

Моменты при пуске и торможении М_пуск = М_торм = 3* М_наг = 1,35 Н*м.

Тип выбранного двигателя постоянного тока: СЛ-661.

Параметры выбранного двигателя:

- номинальная мощность Р_ном = 230 Вт;

- номинальный ток якоря I_{я ном} = 2,9 А;

- номинальная частота вращения n_ном = 2400 об/мин;

- номинальный вращающий момент М_ном = 0,925 Н·м;

- пусковой момент М_{пуск двиг} = 1,55 Н·м;

- статический момент трения М_тр = 0,038 Н·м;

- момент инерции якоря J = 9,35·10^-4 кг·м²;

- сопротивления обмотки якоря R_я = 1,75 Ом.

Е = К·Ф·ω.

М_д = К·Ф·I_я.

М_ном = К·Ф·I_{я ном}.

К·Ф = М_ном / I_{я ном} = 0,925 Н·м / 2,9 А = 0,319 Н·м/А.

I_я  = М_д / 0,319.

Пусковой ток: I_{я max} = М_пуск / 0,319 = 1,35/0,319 = 4,23 А.

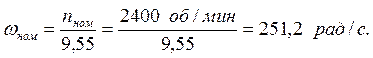
Идуктивность обмотки якоря может быть оценена по эмпирической формуле Уманского:

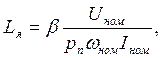
где U_ном, I_ном, ω_ном – номинальные значения напряжения, тока и скорости; p_п – число пар полюсов машины; p_пω_ном – частота тока в обмотке якоря.

Коэффициент β рекомендуется принимать 0,6 для малых машин без компенсации реакции якоря.

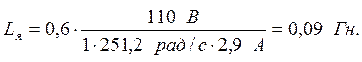
Электромагнитная постоянная времени: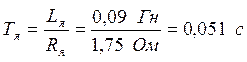

Примем электромеханическую постоянную времени Т_м = 0,5 с. Это означает, что результирующий момент инерции, приведенный к валу двигателя, составляет:

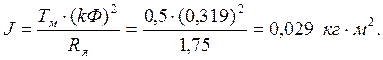
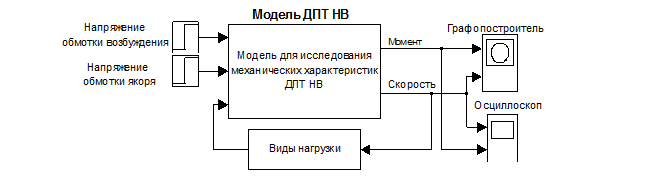
Рис. 1. Модель для изучения принципа работы ДПТ НВ.

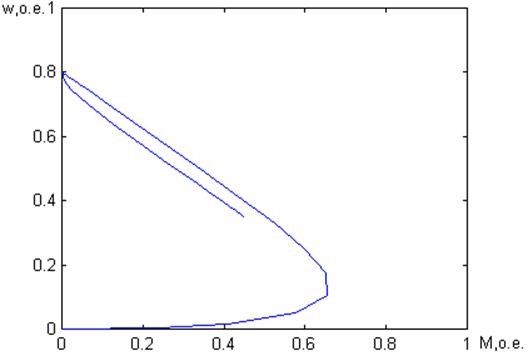
Рис. 2. Механическая характеристика двигателя.

Двигательный режим:

При прикладывании статической нагрузки скорость двигателя снижается из-за падения напряжения в якорной цепи.

 

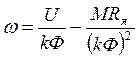
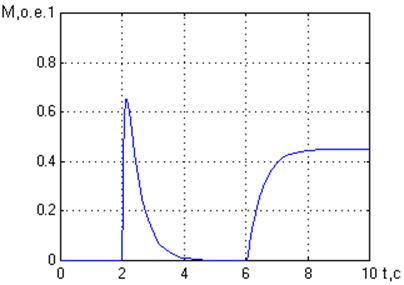
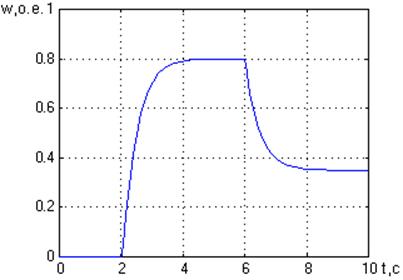
а)                                                                  б)

Рис. 3. Графики переходных процессов в относительных единицах.

а - момента нагрузки; б- скорости двигателя при М = 0,45.

Режим противовключения:

Происходит торможение привода статическим моментом нагрузки превышающим статический момент двигателя. Двигатель совершает реверс и вращается с установившейся скоростью.

 

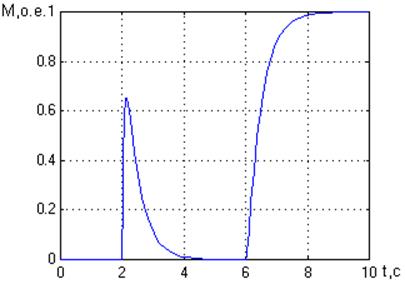
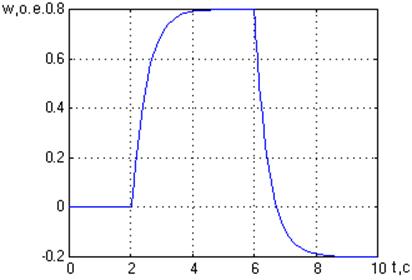
а)                                                                  б)

Рис. 4. Графики переходных процессов в относительных единицах.

а – момента нагрузки; б- скорости двигателя при М = 1.

Генераторный режим:

Если на вал двигателя со стороны механизма станет воздействовать момент не препятствующий, а способствующий движению, то двигатель переходит в генераторный режим.

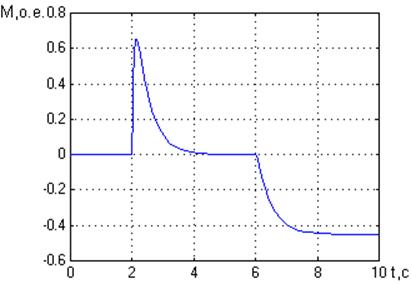
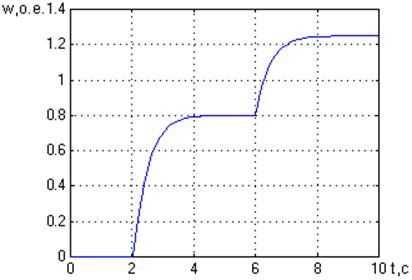
Рис. 5. Графики переходных процессов в относительных единицах.

а – момента нагрузки; б- скорости двигателя при М= - 0,45.

3. Синтез системы управления приводом.

3.1. Функциональная модель электропривода.

Синтезируем систему регулирования скорости ДПТ НВ методом подчиненного регулирования.

Пуск системы осуществляется путем подачи на вход регулятора скорости РС задания скорости. Для снижения динамических выбросов тока выход РС необходимо ограничивать, что достигается настройкой блока ограничения О1 (рис. 6).

По мере разгона двигателя регулятор скорости выйдет из ограничения, его выходная переменная начнет уменьшаться, давая сигнал на уменьшение тока якоря. Установившееся положение, к которому придет система, будет характеризоваться тем, что при данной нагрузке двигателя результирующий входной сигнал РС обеспечит на его выходе значение переменной, которое соответствует данному току нагрузки.

Система во всех режимах будет ограничивать якорный ток значением I_{я max}, которое может быть превышено только в первый момент ограничения РС в результате переходного процесса в токовом контуре.

Также токовый контур должен быстро отрабатывать возмущающее воздействие в виде изменения напряжения сети.

В системе подчиненного регулирования применяют не только стандартные регуляторы, но и стандартные настройки этих регуляторов. В основе стандартной настройки лежит идея синтеза максимально плоских амплитудных характеристик замкнутого контура регулирования, соответствующих фильтрам Баттерворта второго или третьего порядка [2].

Существенным допущением при стандартных настройках является пренебрежение внутренней обратной связью по ЭДС движения. Подобное допущение справедливо, если выполняется условие Т_м + Т_я/5 ≥ 5τ.

Настроим ПИ-регулятор в контуре тока на модульный оптимум.

Объект регулирования контура тока состоит из ШИП и цепи якоря двигателя.

ШИП можно представить апериодическим звеном W_п(p) = K_п / (1 + τp) с малой постоянной времени τ, которая принимается равной периоду коммутации: τ = Т_к.

τ = 0,001 с (частота коммутации f = 1кГц).

K_п = 11.

Передаточная функция объекта управления имеет вид:

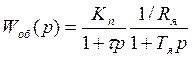
Применим в контуре тока ПИ-регулятор с передаточной функцией :

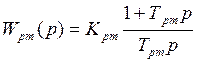
Т_рт = Т_я = 0,051 с.

Коэффициент преобразования цепи обратной связи по току равен К_т. К_т = 1.

К_рт = R_я*Т_я / (2К_п*К_т*τ) = 1,75*0,051 / (2*11*1*0,001) = 4,06.

Настройка на модульный оптимум придает контуру тока динамические свойства, близкие к свойствам звена первого порядка с удвоенной малой постоянной времени:

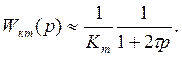   (1)

Объектом регулирования в контуре скорости является оптимизированный контур тока с передаточной функцией (1) и звено, учитывающее механическую проводимость привода. Эта механическая проводимость представляет собой интегрирующее звено.

Передаточная фунция объекта регулирования в контуре скорости имеет вид:

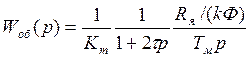
Для получения характеристики фильтра Баттерворта второго порядка применяют П-регулятор скорости с передаточной функцией W_рс(p) = K_рс.

Контур замыкается безынерционной обратной связью по скорости с коэффициентом преобразования К_с = 1.

К_рс = (k*Ф)*К_т*Т_м / (4τ*К_c*R_я) = 0,319*1*0,5 / (0,004*1*1,75) = 22,79.

Ошибка в статическом режиме на превышает:

Δω = (4τ / J)*М_с = 0,062 рад/с.

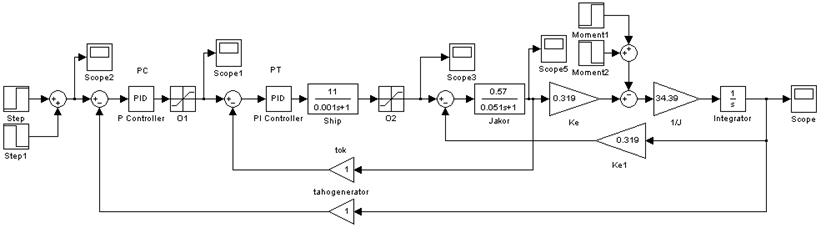
Рис. 6. Система стабилизации скорости.

При задании скорости двигателя 100 рад/с имеем:

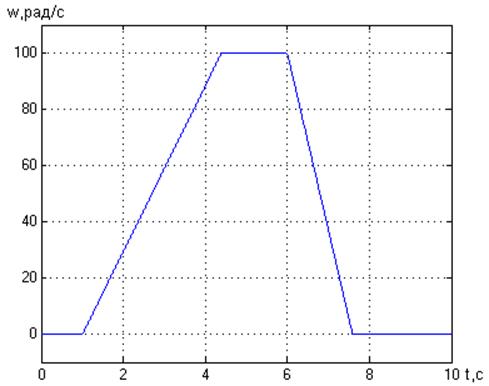
Рис. 7. Зависимость скорости двигателя от времени.

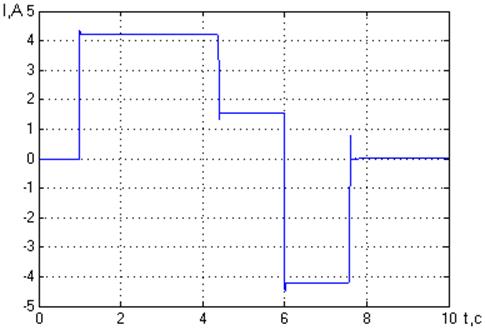
Рис. 8. Диаграмма токов двигателя.

Время пуска: .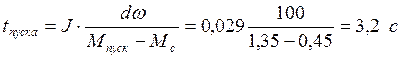

Время торможения: .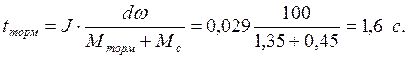

3.2. Виртуальная модель электропривода.

Подставим полученные значения коэффициентов регуляторов контуров тока и скорости в виртуальную модель (рис. 9).

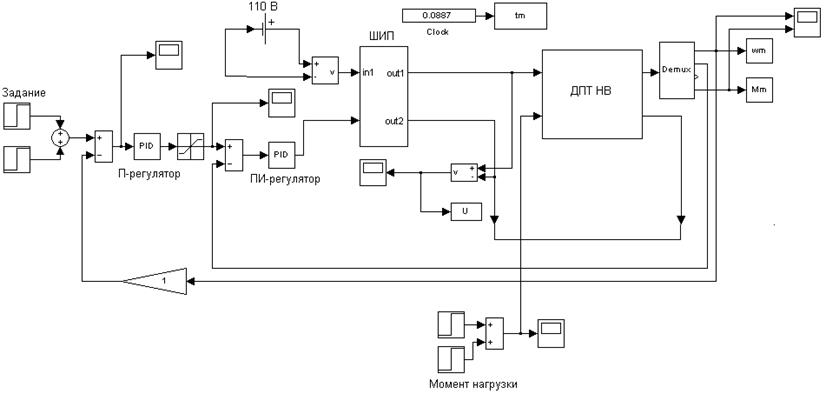
Рис. 9. Виртуальная модель электропривода.

При задании скорости двигателя 100 рад/с имеем:

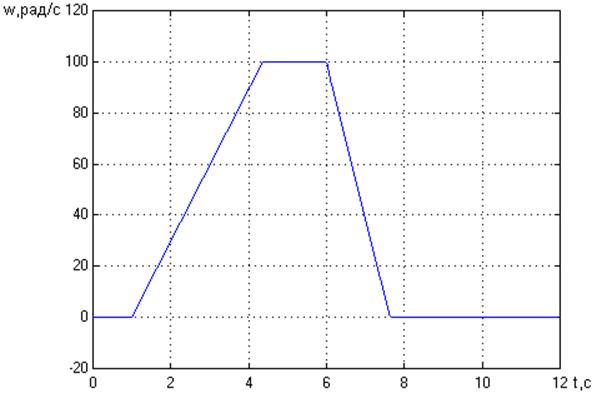
Рис. 10. Зависимость скорости двигателя от времени.

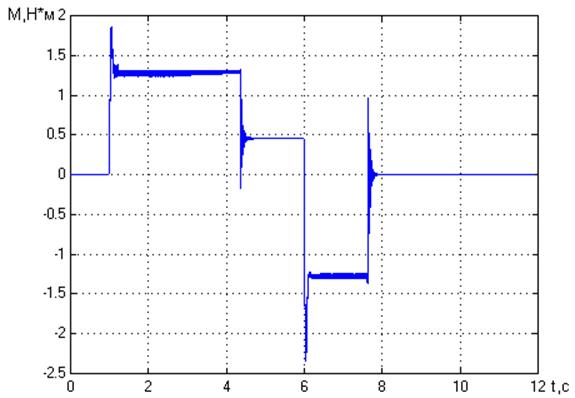
Рис. 11. Нагрузочная диаграмма электропривода.

При виртуальном моделировании имеем схожие результаты, что и при функциональном моделировании.

4. Выводы.

Настройка на модульный оптимум характеризуется небольшим перерегулированием, равным 4,3%. Вследствие малого перерегулирования переходный процесс в оптимизированном контуре тока близок к апериодическому.

Контур скорости с П-регулятором обладает статизмом по возмущающему воздействию – моменту сил статического сопротивления.

5. Литература.

1. Борцов Ю.А., Соколовский Г.Г. Автоматизированный электропривод с упругими связями. -2-е изд., перераб. И доп. – СПб.: Энергоатомиздат. Сантк-Петербург. Отд-ние, 1992.

2. Михайлов О.П. Динамика электромеханического привода металлорежущих станков. М.: Машиностроение, 1989.

3. Ковчин С.А., Сабинин Ю.А. Теория электоропривода: Учебник для вузов. – СПб.: Энергоатомиздат. Санкт-Петербургское отд-ние, 1994.