Информатика и выч. техника \ Проектирование систем управления

Полюса и нули. Полюса и передаточные нули. Передаточные нули и блокирование сигнала. Вычисление передаточных нулей. Блокирующие нули

Страницы работы

9 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Содержание работы

3. ПОЛЮСА И НУЛИ

В многоканальных системах понятие нулей и полюсов существенно многообразнее. Из всего множества нулей здесь будут рассмотрены передаточные и блокирующие нули. Также затронем вопрос вычисления нулей. Вначале обсудим одноканальные системы, а затем многоканальные.

3.1. Полюса и передаточные нули

Определение 3.1. Число (вещественное или комплексное) называют полюсом (pole) правильной рациональной передаточной функции g(s) если его называют нулем (zero) g(s) , если .

Теорема 3.1. Рассмотрим одноканальную систему с правильной передаточной функцией G(s) и несократимой реализацией Тогда число является полюсом g(s) , если и только если существует начальное состояние x₀такое, что при нулевом входе выход системы равен

для некоторой ненулевой постоянной r.

Теорема 3.2. Рассмотрим систему с правильной передаточной функцией g(s) и неприводимой реализацией Если вход u(t) имеет вид , где вещественное или комплексное, не полюс g(s), тогда выход, соответствующий начальному состоянию

и выходу равен для .

Следствие 3.1. Передаточно-блокирующие свойство (transmission- blocking property). Рассмотрим систему с правильной передаточной функцией g(s) и несократимой реализацией Если нуль g(s), тогда реакция на выходе при начальном состоянии и входе тождественно нулевая.

Определение 3.2. Число , вещественное или комплексное, называют полюсом (pole) правильной рациональной матрицы G(s), если и только если он является корнем detD(s), где D(s) – матрица – знаменатель любого правого или левого разложения G(s).

Аналогично теореме 3.1., мы можем сформулировать теорему, характеризующую полюса G(s).

Теорема 3.3. Рассмотри многомерную систему с правильной передаточной матрицей G(s) и некоторой неприводимой реализацией Тогда число будет полюсом G(s), если и только если существуют начальные условия x₀ такие, что реакция системы на выходе при нулевом входе равна для некоторого ненулевого вектора r.

Отметим, что каждый полюс G(s) должен быть полюсом некоторого элемента G(s) , и каждый полюс каждого элемента G(s) должен быть полюсом G(s). Далее будем считать, что правильная рациональная матрица G(s) размером q*p имеет полный ранг в поле рациональных функций. Это означает, что если q ≤ p, то rang G(s)=q. Если же q ≥ p, то rang G(s)=p. Если G(s) не полного ранга в поле рациональных функций, тогда существует 1*q рациональный вектор M(s) или p*1 рациональный вектор P(s) такой, что

M(s) G(s)=0 или G(s) P(s)=0.

Если умножим (3.1) на наименьший общий знаменатель M(s) или P(s), они преобразуются к

или ,

где и полиномиальные векторы. Так как мы имеем для всех возможных входов. Это влечет за собой то, что число эффективных выходов меньше чем q. Аналогично, если и если введем в систему предкомпенсатор , то для всех возможных выходов u(s) имеем . Отсюда следует, что число эффективных входов меньше, чем p. Рассмотрим свойства G(s) со следующими взаимно простыми разложениями:

(3.2)

Если G(s) имеет полный ранг в поле рациональных функций, то таковыми являются и N₁(s) и N_r(s). Таким образом, что для почти всех из ℂ, комплексные матрицы N₁(s) и N_r(s) имеют ранг в поле комплексных чисел.

Определение 3.3. Рассмотрим q*p правильную рациональную функцию G(s) с взаимно простым разложением , Предполагаем, что G(s) и, следовательно, N₁(s)имеют полный ранг (в поле рациональных функций). Тогда число , вещественное или комплексное, называют передаточным нулем (transmission zero) G(s) Если и только если rangN₁(s)<min (p,q), в ℂ, поле комплексных чисел.

Пример 3.1. Рассмотрим левое взаимно простое разложение

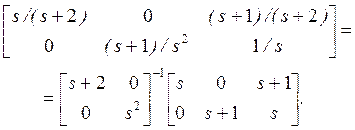
Матрица N₁(s) имеет ранг 2 Для каждого s из ℂ; следовательно, G₁(s) не имеет передаточных нулей.

Пример 3.2. Рассмотрим левое взаимно правое разложение

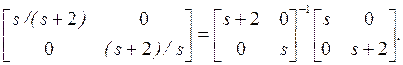
данная матрица N₁(s) ранга 1 для s=0 и s=-2. Следовательно, 0 и –2 два передаточных нуля G(s). Отметим, что 0 и –2 также и полюса G₂(s).

Можно показать, что существуют унимодальные матрицы V(s) и U(s) такие, что

N₁(s)= U(s)N_r(s)V(s). (3.3)

Следовательно, передаточные нули могут быть определены из N₁(s) и N_r(s). Отметим, что если матрицы N₁(s) и N_r(s) квадратные, то передаточные нули G(s) есть корни detN₁(s) или detN_r(s). Как видно из примеров, передаточные нули могут быть равными полюсам G(s). Хотя некоторые элементы G(s) могут иметь нули, G(s) может не иметь их. Передаточные нули квадратной матрицы могут отличаться от нулей detG(s).

Теорема 3.4. рассмотрим многоканальную систему с q*p правильность рациональной матрицей G(s) несократимой представлением

Если вход u(t) взят в виде , где - вещественное или комплексное число и не является полюсом G(s) и к произвольный p*1 столбцовый вектор, тогда выход, соответствующий этому входу и начальному состоянию , равен

3.2. Передаточные нули и блокирование сигнала

Подстановка в (H-6) дает

где N₁(s) p*q полиномиальная матрица полного ранга. Рассмотрим отдельно случай q ≥ p и случай q < p.

Случай 1: q ≥ p.

В этом случае rangN₁(s) = p в ℝ (s) по предположению. Тогда rangN₁(s) = p в ℂ для всех из ℂ за исключением передаточных нулей G(s). Если передаточный нуль, тогда rangN₁(s) < p. Следовательно, существует p*1 ненулевой постоянный вектор k такой, что N₁()k=0 и соответственно

(3.5)

Случай 2: q < p.

В этом случае имеем rangN₁(s) =q в ℝ (s) по предположению. Тогда для любого в ℂ имеем rangN₁()≤q < p в ℂ. Следовательно, существует ненулевой k такой, что N₁()k=0

(3.6)

Так как это уравнение имеет место для всех в ℂ, оно не может быть использовано для характеризации передаточных нулейG(s) в случае q ≥ p. По этой причине, мы должны рассматривать этот случай отдельно от случая q ≥ p. Если q < p , тогда является передаточным нулем G(s), если и только если существует ненулевой числовой 1*p вектор h такой, что