Нули и полюса многомерной системы. Минимальная реализация, степень Макмиллана, столбцовая/строчная приведенность, передаточные нули

3.  НУЛИ   И  ПОЛЮСА  МНОГОМЕРНОЙ  СИСТЕМЫ

Минимальная реализация, степень Макмиллана, столбцовая / строчная приведенность, передаточные нули.

Вводится понятие нулей и полюсов для многомерных систем. Рассмотрен переход от полиномиального описания к описаниям в пространстве состояний (называют ¢реализацией¢). Указана связь между левым и правым разложениями передаточной функции, между взаимной простотой разложения и управляемостью / наблюдаемостью. Раскрыт физический смысл нулей. Введено понятие нулей и полюсов в бесконечности, имеющих важное значение в синтезе. Раскрыты их свойства. Приведен интересный пример перехода от полиномиального описания к описанию в пространстве состояний ($18). Обратите внимание на S44, S49, S50, S55, S60, S61, S62, $16. Доказательства в S50, S51, S53а, S54, S59, S60, S61 при первом чтении можно опустить.

S44.  Для  найдем форму Смита-Макмиллана :

.

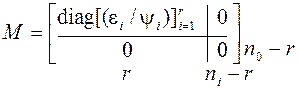Любой корень любого полинома y_i называют полюсом (pole) H. Множество полюсов матричной передаточной функции H обозначают P[H]. Любой корень любого полинома e_i называют нулем (zero) матричной передаточной функции H и множество их обозначают Z(H).

$14.  Найти нули и полюса передаточной функции:

.

(Ответ: нули: “-1”, полюса: ”-1”. Когда в одноканальной системе полюс  может совпадать с нулем?)

S45.  Элементы матрицы H обозначим h_{i j}, т.е. H = [h_{i j}], где . Справедливы следующие утверждения:

1)  .

Эта запись читается следующим образом: р является полюсом Н тогда и только тогда, когда существует элемент h_{i j} матрицы Н такой, что р есть полюс h_{i j}. Двоеточие ²:² читается ²такой, что²;

2)  р Ï Р[Н] Û отображение ²s ® H(s)² ограничено в достаточно малой окрестности р Î С.

С – плоскость комплексной переменной. Использовано обозначение ²s ® H(s)². Поясним его на примере: функция sin(x) в этой записи выглядит так “x ® sin(x)”.

S46.  Дано: ; rk H  min(n₀, n_i), (N_r, D_r), (D_l, N_l) – правое и левое взаимно простые разложения Н. Тогда:

1)  p Î P[H] Û det D_r(p) = 0 Û det D_l(p) = 0;

2)  z Î Z[H] Û rk N_r(z) < r Û rk N_l(z) < r;

3)  для H и нули и полюса меняются местами:

z Î Z[H] Û z Î P[]; p Î P[H] Û p Î Z[].

S47.  Описание системы в пространстве состояний (state space system description):

x = Ax + Bu,       y = Cx + Du.

Возможна краткая запись: [A, B, C, D]. Несложно найти передаточную функцию:  H(s) = C(sI – A)^-1B + D. Обычно полагают, что:

 .

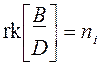Здесь n₀ – размерность вектора y; n_i – размерность вектора u. Нарушение первого условия приводит к линейной зависимости выходов и нарушение второго условия – к линейной зависимости входов, что обычно неудобно. По заданной передаточной функции Н возможен подбор матрицы А различных размеров. Поиск [A, B, C, D] по H называется реализацией (realization) H. Случай реализации А наименьших размеров называется минимальной реализацией (minimal realization).

S48.  Дано , пусть [A, B, C, D] – минимальная реализация порядка . Кроме того:

rk [C | D] = n₀,  .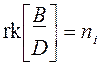

Тогда:

1)  p Î P[H] Û det (pI – A) = 0;

2)  пусть дана системная матрица

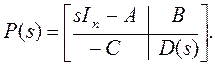
Справедливо следующее утверждение:

                               z Î Z[H] Û rk P(z) < n + min (n₀, n_i).                                            (а)

Для доказательства этих утверждений потребуются дополнительные рассуждения, которые будут приведены в S49, S50, S51. Доказательство 1) дано в S53.

S49.  Справедливо:

1)  (А, В) управляемая (controllable) Þ (sI – A)^-1B – левое взаимно простое разложение пары (А, В);

2)  (С, А) наблюдаемая (observable) Þ С(sI – A)^-1 – правое взаимно простое разложение пары (С, А).

S50.  Правое (N_r, D_r) и левое (D_l, N_l) взаимно простые разложения некоторой матрицы H(s) связаны соотношением S30:

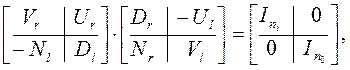                                                                    (а)

где V_r, U_r, V_l, U_l – унимодальные матрицы. В качестве левого разложения в (а) можем взять в соответствии с 1) из S49 (D_l, N_l) = ((sI – A), B):

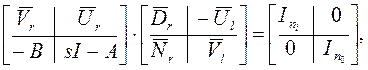                                                                (б)

где унимодальные матрицы обозначены так:`V<sub>r</sub>,`U_r,`V<sub>l</sub>,`U_l. Правое взаимно простое разложение, соответствующее левому разложению ((sI – A), B) обозначено (N_r, D_r), откуда

                                                   (sI – A)^-1B =                                                  (в)

В (а) за правое взаимно простое разложение в соответствии с 2) изS49 можем принять (N_r, D_r) = (С, (sI – A)):

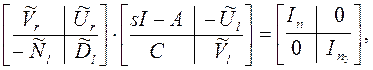                                                                (г)

где  - унимодальные матрицы;  - левое взаимно простое разложение, соответствующее правому разложению С(sI – A)^-1.