Нули и полюса многомерной системы. Минимальная реализация, степень Макмиллана, столбцовая/строчная приведенность, передаточные нули, страница 2

Утверждается следующее:  - правое взаимно простое разложение для С(sI – A)^-1В.

Д о к а з а т е л ь с т в о. Из (г) и (б) следует

                                             ,                                                   (д)

                                                .                                                       (е)

Умножим (д) справа на (sI – A)^-1В:

Используем (в): . После умножения справа на `D_r получим:

. Полученное разложение для`N_r подставим в (е):

Перегруппируем члены

В скобках выделены унимодальные матрицы. Получили тождество Безу S23. Следовательно, в соответствии с S28 пара матриц  - правое взаимно простое разложение для С(sI – A)^-1В. Действительно, если используем (в), получим  = =.

S51.  Покажите, что если возьмем исходные данные те же, что и в S50, то  - правое взаимно простое разложение.

S52.  Исходные данные – те же, что и в S50. Утверждается, что

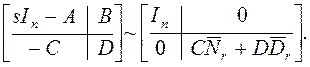                                                                           (а)

Д о к а з а т е л ь с т в о. Из (S50,б) находим:

                          -, .                                (б)

Покажем, что матрицы

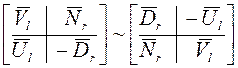                                                                                         (в)

подобны. Произведем ряд элементарных преобразований над правой частью (в):

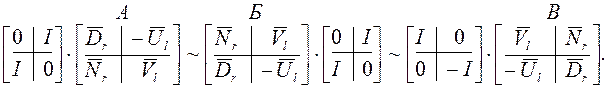
Элементарные преобразования состоят в следующем: в матрице А переставили строки – получили матрицу Б; в матрице Б переставили столбцы – получили матрицу В; если в матрице В во второй строке изменим знак – получим левую матрицу в (в). Соотношение (в) доказано. Приступим к доказательству (а): левую матрицу из (а) умножим на левую (унимодальную!) матрицу из (в):

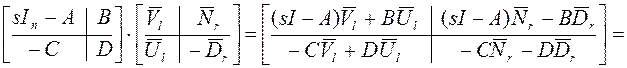
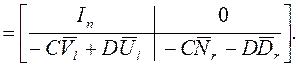                                                                              (г)

В последнем равенстве использовано (б). Последняя матрица подобна правой матрице (а).

$15.  Докажите, что последняя матрица в (г) из S52 подобна правой матрице в (а) из S52. (Подсказка: первую строку умножить на  и сложить со второй.)

S53.  Д о к а з а т е л ь с т в о утверждения 1) из S48.

Для передаточной функции H(s) справедливо утверждение

                                          p Î P[H] Û det D_r(p) = 0,                                                (а)

где D_r(p) – ²знаменатель² любого правого взаимно простого разложения S46. В S50 доказали, что для Н = С(sI – A)^-1B матрица  - ²знаменатель² взаимно простого правого разложения. В (а) в качестве D_r(p) возьмем . Получим:

                                          p Î P[H] Û det ,                                             (б)

²Знаменатели² любых разложений имеют одни и те же корни, что следует из второго утверждения S33. Но в (в) S50 показано, что в качестве знаменателя можем взять , следовательно,

                                      det Û .                                       (в)

Из (б) и (в) следует p Î P[H] Û det(sI –A) = 0, что и требовалось доказать.

Д о к а з а т е л ь с т в о утверждения 2) из S48. Из 2) S46:

z Î Z[H] Û rk N_r(z) < min(n₀, n_i).

Согласно S51:  - ²числитель² правого разложения, тогда

                              z Î Z[H] Û rk[] < min(n₀, n_i).                                   (г)

По утверждению S52:

                        ранг системной матрицы = n + rk[].                           (д)

Из (г) и (д) следует:

rk[] < min(n₀, n_i) Û rk[P(z)] < n + min(n₀, n_i)

что и требовалось доказать.

S53а. Пусть [А, В, С, 0] - минимальная реализация H Î , rk[B] = n_i, rk[C] = n₀. Тогда:

1)  нули инвариантны при переходе к новому базису:

;

2)  нули инвариантны при введении пропорциональной обратной связи по выходу (constant output feedback):

A ¬ A + BKC,  B ¬ B,  C ¬ C.

Д о к а з а т е л ь с т в о. Докажем 1):

z Î Z[H] Û rk P(z) < n + min(n₀, n_i)

следует из S48, 2). Но

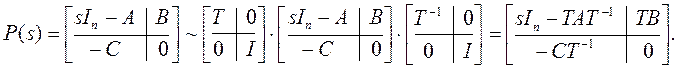
При подобных преобразованиях ранг матрицы не меняется. Утверждение 1) доказано.

Для доказательства 2) достаточно применить унимодальное преобразование над строчками матрицы P(z):

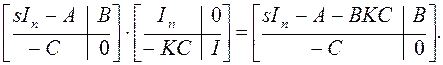
Аналогично при унимодальных преобразованиях ранг не меняется. Следовательно, утверждение 2) доказано.

S54.  Пусть для H Î  четверка матриц [А, В, С, 0] - минимальная реализация. Кроме того, пусть rk(В) = n_i, rk(C) = n₀. Тогда имеет место:

1)  при  тогда и только тогда, когда , такие, что

                                          (A + BK)x₀ = zx₀,  Cx₀ = 0;                                                (а)

2)  при  тогда и только тогда, когда  такие, что

                                         .                                           (б)

Поясним данные утверждения. Формулы (а) эквивалентны