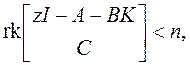 (в)
(в)
что равносильно утверждению: “z – ненаблюдаемое собственное значение”. Покажем это. Так как H = C(zI – A – BK)-1, то пару матриц С, (zI – A – BK) можно рассматривать как правое разложение, но не взаимно простое ввиду предыдущего неравенства. Следовательно, есть матрица R(s), не унимодальная и входящая в обе матрицы разложения, которая сокращается при вычислении H.
Таким образом, утверждение 1) можно сформулировать так: “для любого нуля z существует обратная связь по состоянию К такая, что в системе нуль z оказывается ненаблюдаемым собственным значением”.
Формулы (б) эквивалентны:
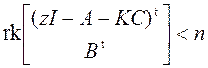 ,
,
т.е. z – неуправляемое собственное значение. Утверждение 2) формулируется так: для всякого нуля z существует обратная связь по выходу К такая, что в системе (с обратной связью!) z оказывается неуправляемым собственным значением.
Д о к а з а т е л ь с т в о утверждения 1). Покажем, что из формулы (а), равносильной (в), следует z Î Z[H]. Но (в) эквивалентно
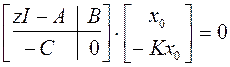 ,
,
т.е. z – нуль для Н:
системная матрица при заданном z такова, что ранг ее понижен при векторе ![]() . Показали, что z Î Z[H].
. Показали, что z Î Z[H].
Покажем, что из z Î Z[H] следует (а). Пусть z Î Z[H]. Тогда rkP(z)<n + +min(n0,ni). Следовательно, существуют такие х0, u0, что
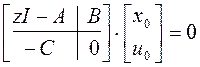 .
(г)
.
(г)
Так как [А, В, С, 0] - минимальная реализация, то rk B = ni (кстати, rk C = n0)
откуда $ Bl такая, что BlB = ![]() . Из
(г) найдем:
. Из
(г) найдем:
(zI – A)x0 + Bu0 = 0. (д)
Умножим слева на Bl: Bl(zI – A)x0 + u0 = 0.
Обозначим Bl(zI – A) через К (z - число!).
Получим ![]() , откуда
, откуда ![]() .
Найденное u0 подставим в (д):
.
Найденное u0 подставим в (д):
![]()
![]() . Это равносильно (А + ВК)х0 = zх0. Из (г) сразу же следует Сх0 = 0.
Соотношения формулы (а) доказаны.
. Это равносильно (А + ВК)х0 = zх0. Из (г) сразу же следует Сх0 = 0.
Соотношения формулы (а) доказаны.
S55. Пусть ![]() . Нули и полюса Н на бесконечности (poles and zeros at infinity) – это нули и полюса отображения l ® Н(l-1) при l = 0. Например отображение l ® l-1 дает соответствие: l = 0 ® l-1= ¥.
. Нули и полюса Н на бесконечности (poles and zeros at infinity) – это нули и полюса отображения l ® Н(l-1) при l = 0. Например отображение l ® l-1 дает соответствие: l = 0 ® l-1= ¥.
$16. Показать справедливость:
1)
если![]() -
невырожденная и столбцово приведенная полиномиальная матрица, то D не имеет нулей в бесконечности;
-
невырожденная и столбцово приведенная полиномиальная матрица, то D не имеет нулей в бесконечности;
2)
пусть ![]() . Н правильная
тогда и только тогда, когда Н не имеет
полюсов в ¥;
. Н правильная
тогда и только тогда, когда Н не имеет
полюсов в ¥;
3)
пусть ![]() -
невырожденная. D не имеет нулей в
бесконечности тогда и только тогда, когда
-
невырожденная. D не имеет нулей в
бесконечности тогда и только тогда, когда ![]() правильная.
правильная.
S56. Пусть ![]() . Максимальная степень миноров всех
порядков матрицы D называется степенью Макмиллана
(McMillan degree) и обозначается
. Максимальная степень миноров всех
порядков матрицы D называется степенью Макмиллана
(McMillan degree) и обозначается ![]() .
.
S57. ![]() - допустим, невырожденная полиномиальная матрица. В
этом случае D не имеет нулей в ¥ тогда и только тогда, когда степень определителя матрицы D равна степени Макмиллана.
- допустим, невырожденная полиномиальная матрица. В
этом случае D не имеет нулей в ¥ тогда и только тогда, когда степень определителя матрицы D равна степени Макмиллана.
![]() (а)
(а)
$17. У матрицы
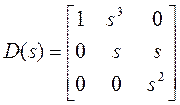
равенство (а) из S57 не выполняется, следовательно, D имеет нули в ¥.
S58. Пусть ![]() – столбцово
приведенная (colomn reduced), где D,
RÎ
– столбцово
приведенная (colomn reduced), где D,
RÎ![]() , D – невырожденная (nonsingular), R – унимодальная. Тогда D не имеет нулей в ¥ (D правильная !) тогда и только тогда, когда
, D – невырожденная (nonsingular), R – унимодальная. Тогда D не имеет нулей в ¥ (D правильная !) тогда и только тогда, когда ![]() .
.
Доказательство несложно. Из определения D1 имеем ![]() , т.е.
, т.е. ![]() - правое разложение передаточной функции
- правое разложение передаточной функции ![]() . Если
воспользоваться S41, получим, что
. Если
воспользоваться S41, получим, что ![]() правильная,
откуда (см. $$16, 3) следует, что D
– правильная и искомое утверждение доказано.
правильная,
откуда (см. $$16, 3) следует, что D
– правильная и искомое утверждение доказано.
S59. ![]() - так обозначим
изображение передаточной функции. Пусть
- так обозначим
изображение передаточной функции. Пусть ![]() . Тогда
существует управление
. Тогда
существует управление
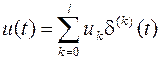 (а)
(а)
такое, что
![]()
где оригинал ![]() равен
равен
![]() .
(б)
.
(б)
Здесь ![]() – k-я производная
дельта-функции и в изображениях (а)
имеет вид
– k-я производная
дельта-функции и в изображениях (а)
имеет вид 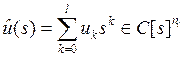 . Можно сказать, что управление u(t) (а) ²создает² начальные условия для
. Можно сказать, что управление u(t) (а) ²создает² начальные условия для ![]() такие, что при
такие, что при ![]() имеет место (б).
имеет место (б).
Д о к а з а т е л ь с т в о. Найдем правое взаимно
простое разложение ![]() матричной передаточной функции
матричной передаточной функции ![]() . Тогда
. Тогда
![]() (в)
(в)
имеет полный столбцовый ранг. Если р – полюс ![]() , тогда
, тогда ![]() . Следовательно, существует
. Следовательно, существует ![]() такое, что
такое, что
![]() .
(г)
.
(г)
Из (в) и
последнего равенства имеем ![]() . Управление выберем
. Управление выберем ![]() . Ввиду (г)
. Ввиду (г) ![]() . При выбранном управлении выход
. При выбранном управлении выход
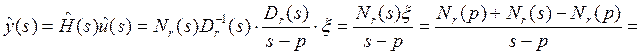
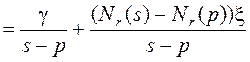 .
.
Если второй член обозначить через ![]() и прейти к оригиналам, получим (б).
и прейти к оригиналам, получим (б).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.