S60. Возьмем передаточную функцию ![]() , ni £ n0. Пусть
, ni £ n0. Пусть ![]() . Тогда существуют вектор
. Тогда существуют вектор ![]() и вектор
и вектор ![]() такие,
что
такие,
что
![]() (а)
(а)
и выход ![]() . В оригиналах
. В оригиналах ![]() , где
, где ![]() .
.
Прокомментируем утверждение. ![]() в
оригиналах соответствует набор d импульсов и их
производных, т.е. для
в
оригиналах соответствует набор d импульсов и их
производных, т.е. для ![]() . Для n(t) тоже можем сказать, что это набор производных d импульсов, если вспомним, что
. Для n(t) тоже можем сказать, что это набор производных d импульсов, если вспомним, что ![]() - полином от s. Таким образом,
утверждается, что если z – ноль и выбран
вход вида (а), то на выходе для
- полином от s. Таким образом,
утверждается, что если z – ноль и выбран
вход вида (а), то на выходе для ![]() получим 0. Такой входной сигнал
блокируется, и поэтому нули z называют передаточными нулями (zero of
transmission).
получим 0. Такой входной сигнал
блокируется, и поэтому нули z называют передаточными нулями (zero of
transmission).
Д о к а з а т е л ь с т в о. Возьмем левое взаимно
простое разложение ![]() для
для ![]() . Тогда
существуют унимодальные матрицы
. Тогда
существуют унимодальные матрицы ![]() такие, что
такие, что
![]() .
(б)
.
(б)
Возьмем ноль передаточной функции ![]() . Тогда по 2) из S46
. Тогда по 2) из S46 ![]() . Следовательно,
. Следовательно, ![]() $ такой, что
$ такой, что ![]() . Определим вектор
. Определим вектор
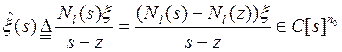 .
(в)
.
(в)
Приступим к выбору второй компоненты вектора управления u(t) (а):
![]() ,
, 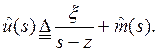
Тогда
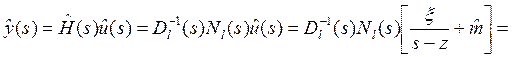
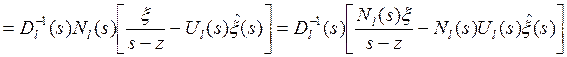
Воспользуемся (в) и (а):
![]()
Видим, что ![]() - полиномиальный
вектор, т.к.
- полиномиальный
вектор, т.к. ![]() – унимодальная и
– унимодальная и ![]() -
полиномиальная (в).
-
полиномиальная (в).
S61. Пусть ![]() ,
, ![]() ,
, ![]() Возьмем
Возьмем
![]() ,
, ![]() . Тогда
существует вектор
. Тогда
существует вектор ![]() ,
, ![]() такой,
что для всякого
такой,
что для всякого ![]() ,
, ![]() существует
полиномиальный вектор
существует
полиномиальный вектор ![]() такой, что если возьмем вход
такой, что если возьмем вход
![]()
то выход ![]() будет таким, что
удовлетворится условие
будет таким, что
удовлетворится условие ![]() для "t ³ 0.
для "t ³ 0.
К о м м е н т а р и й. Можно сказать, что передача
сигнала ![]() блокируется на выходе в направлении
вектора h.
блокируется на выходе в направлении
вектора h.
Д о к а з а т е л ь с т в о. Пусть ![]() – левое взаимно простое разложение Н. Возьмем
– левое взаимно простое разложение Н. Возьмем ![]() . Тогда (S46)
. Тогда (S46) ![]() . Следовательно, существует вектор
. Следовательно, существует вектор ![]() такой, что
такой, что
![]() .
(а)
.
(а)
Ввиду взаимной простоты разложения ![]()
![]() . Из (а) следует
. Из (а) следует
![]() (б)
(б)
Возьмем произвольный вектор ![]() :
:
![]() (в)
(в)
Так как ![]() с учетом (а)
с учетом (а) ![]() , то
, то ![]() можно рассматривать как передаточную функцию.
Найдем взаимно простое разложение (n, d):
можно рассматривать как передаточную функцию.
Найдем взаимно простое разложение (n, d):
![]() .
(г)
.
(г)
Тогда так как![]() , то
, то
![]() (д)
(д)
Ввиду ![]() такое, что
такое, что ![]() . Поэтому
. Поэтому
![]() .
.
Можем приступить к конструированию управления: выберем
![]() (е)
(е)
![]()
![]() (ж)
(ж)
Вычислим произведение ![]() :
:
![]()
![]()
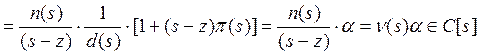 .
.
Здесь использованы последовательно (б), (ж), (в), (г), (е), (д). Показали, что
![]() .
.
В оригиналах это соответствует ![]() ,т.е. для
,т.е. для ![]()
![]() .
.
S62. Рассмотрим переход от полиномиального описания к описанию в пространстве состояний. Дано представление
![]() (а)
(а)
или кратко ![]() . Пусть соответствующая
передаточная функция
. Пусть соответствующая
передаточная функция ![]() будет
строго правильная, что соответствует условию
будет
строго правильная, что соответствует условию
![]() .
.
Степень столбца j
матрицы Nr не больше степени
столбца j матрицы Dr, которую обозначили через kj. Пусть Dr – столбцово приведенная, т.е. ![]() , где ni – число входов. Рассмотрим вопрос перехода от
, где ni – число входов. Рассмотрим вопрос перехода от ![]() к описанию в пространстве состояний [А, В, С, 0]:
к описанию в пространстве состояний [А, В, С, 0]:
![]() .
.
Разложим матрицы Dr(р) и Nr(р):
![]()
![]() (б)
(б)
где Dh – матрица коэффициентов при высших (highest) степенях (по столбцам), Dl – коэффициентная матрица, матрицы S(p) и Y(p) таковы:
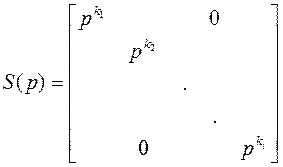 ,
, 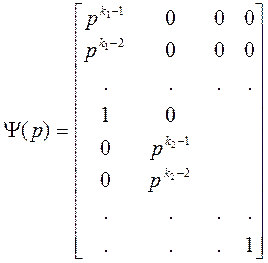 .
.
Подставим (б) в (а):
![]() ,
,
(в)
![]() .
.
Введем вектор состояния
![]() (г)
(г)
Фактически все необходимые соотношения приведены. Дальнейшие пояснения смотрите в примере.
$18. Найти минимальную реализацию (А, В, С) для системы, описываемой полиномиальными матрицами:
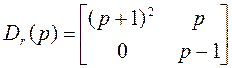 ,
, 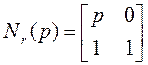 .
.
Здесь n0 = 2, ni = 2. Степень столбца 1 равна 2, степень столбца 2 равна 1: k1 = 2, k2 = 1,
откуда n = k1 + k2 = 3. С
другой стороны, ![]() . Следовательно, матрица Dr(p) – столбцово приведенная.
Несложно проверить, что передаточная функция строго правильная. Выпишем
соответствующие матрицы:
. Следовательно, матрица Dr(p) – столбцово приведенная.
Несложно проверить, что передаточная функция строго правильная. Выпишем
соответствующие матрицы:
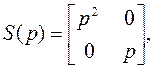
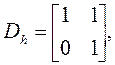
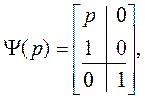
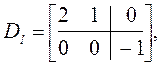
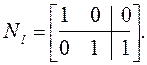
Действительно:
![]()
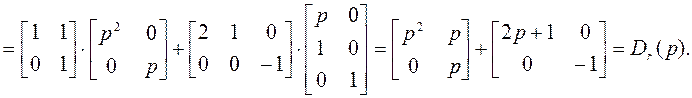
Воспользуемся соотношениями (в) из S62:
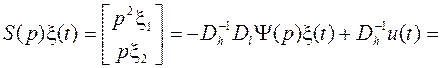
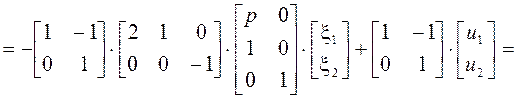
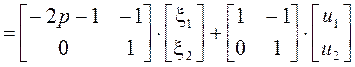 (а)
(а)
и (г) из S62:
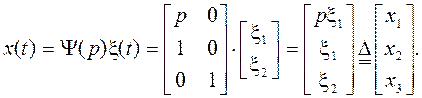
Таким образом, получили
![]() .
(б)
.
(б)
Из (а) следует:
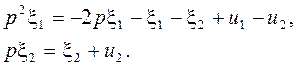
Учтем (б):
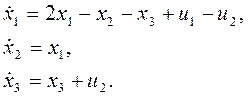
Следовательно,
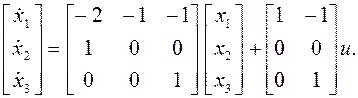
Нашли матрицы А, В. Найдем матрицу С по формуле (в) из S62:
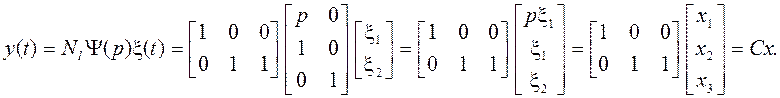
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.