Информатика и выч. техника \ Проектирование систем управления

Моделирование электроприводов

Страницы работы

11 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Фрагмент текста работы

Министерство образования и науки РФ

Новосибирский Государственный Технический Университет

Кафедра Автоматики

Лабораторная работа №1:

Моделирование электроприводов факультет: АВТ группа: АА-16 Проверил: студент: Старченко А. Кондратьев В. А.

Новосибирск

2005

Задание

Для выполненного в прошлом семестре проекта необходимо разработать схемы управления, реализованные на базе управляемого выпрямителя и широтно-импульсного преобразователя.

- под заданный график изменения нагрузки с целью уточнения эквивалентных значений моментов и токов по «гладкой составляющей»;

- под выбранные вид и параметры настройки регулятора в различных режимах работы в разомкнутой и замкнутой системах;

Параметры выбранного двигателя

Исходные данные:

Вариант работы определяется по номеру зачетной книжки – NL (24).

Таблица 1 . Численные значения тахограммы

N	Ω₁	Ω₂	Ω₃	Ω₄	Ω₅	Ω₆	Ω₇
2	75	100	-100	150	-150	100	-75
Ω – текущая частота вращения двигателя Таблица 2. Временные параметры тахограммы
L	t₁	t₂	t₃	t₄	t₅	t₆	t₇
4	1	5	1	5	1	5	1

t_i (cек) – текущее время работы двигателя на установившейся частоте вращения - W_i_.

Время паузы t_п в работе двигателя для всех вариантов – 0,5 сек.

Момент нагрузки – реактивный.

М_наг. = 0.3 Н*м – чётный вариант.

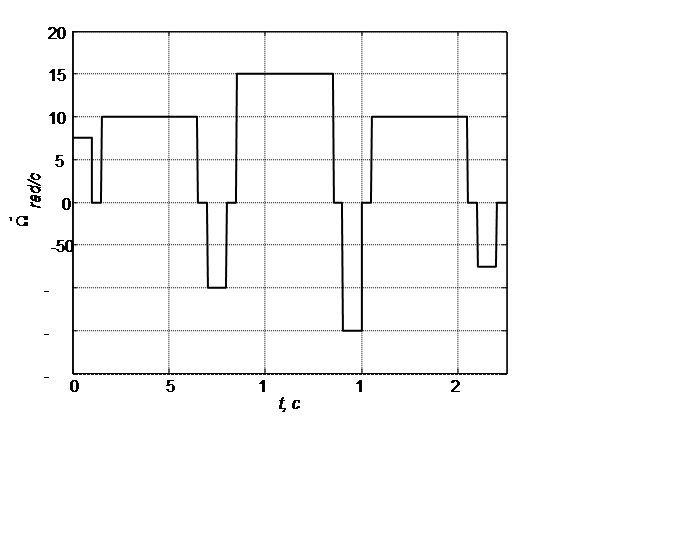
Рис 1. Тахограмма двигателя

Момент нагрузки – реактивный. М_наг = 0,3 Н*м.

Моменты при пуске и торможении М_пуск = М_торм = 3* М_наг = 0.9 Н*м.

Тип выбранного двигателя постоянного тока: СЛ-321

Основные технические данные на ДПТ СЛ-321:

- номинальное напряжение, В:........................ 110;

- номинальная мощность, Вт:....................... 50;

- номинальный ток возбуждения, А:.............. 0,8;

- номинальный ток якоря, А:.......................... 0,85;

- номинальная частота вращения, об/мин:... 3000;

- номинальный вращающий момент,:.... 0,16;

- момент инерции якоря,:...................... 0,00007;

- пусковой момент,:................................ 0,4;

- статический момент трения, :.......... 0,013;

- сопротивление обмотки возбуждения, Ом:..... 1160;

- сопротивление обмотки якоря, Ом:........... 20.5;

- коэффициент самоиндукции якоря:............ 115.

Индуктивность якоря может быть ориентировочно найдена по формуле:

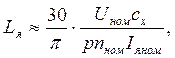
где U_ном– в В; n_ном – в об/мин; I_яном – в А; сx – эмпирический коэффициент

(сx = 0.4 для машин без компенсационной обмотки, сx = 0.1 для машин с компенсационной обмоткой); Lя – в Гн.

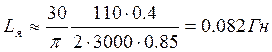
Разработка функциональной модели ДПТ НВ выполняется под вид уравнений, приведенных ниже

где

- относительные переменные состояния двигателя:

;

- параметры двигателя:

Математическое описание модели требует нахождения электромагнитных и электромеханических параметров машины. Для описания ДПТ требуется определить электромеханическую и электромагнитную постоянную времени.

Постоянная времени обмотки якоря: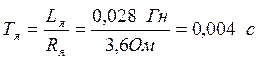

Постоянная времени обмотки возбуждения: 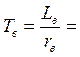0.00007 c

Электромагнитная постоянная времени: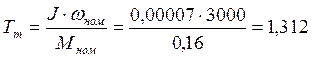

Е = К·Ф·ω.

М_д = К·Ф·I_я.

М_ном = К·Ф·I_{я ном}.

К·Ф = М_ном/ I_{я ном} = 0,16 Н·м / 085 А = 0,188 Н·м/А.

I_я= М_д / 0,188.

Пусковой ток: I_я_max= М_пуск / 0,188 = 0,9/0,188 = 4,78 А.

Это означает, что результирующий момент инерции, приведенный к валу двигателя, составляет:

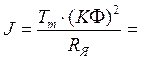
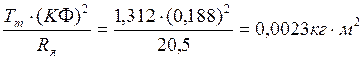
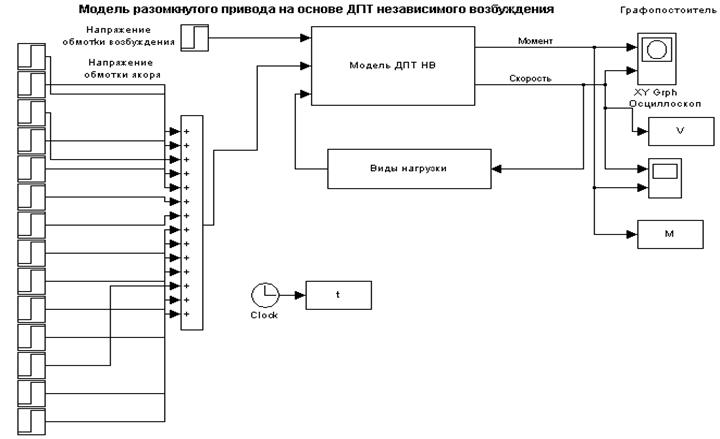
Рис.2. Модель для изучения принципов работы двигателя

постоянного тока независимого возбуждения.

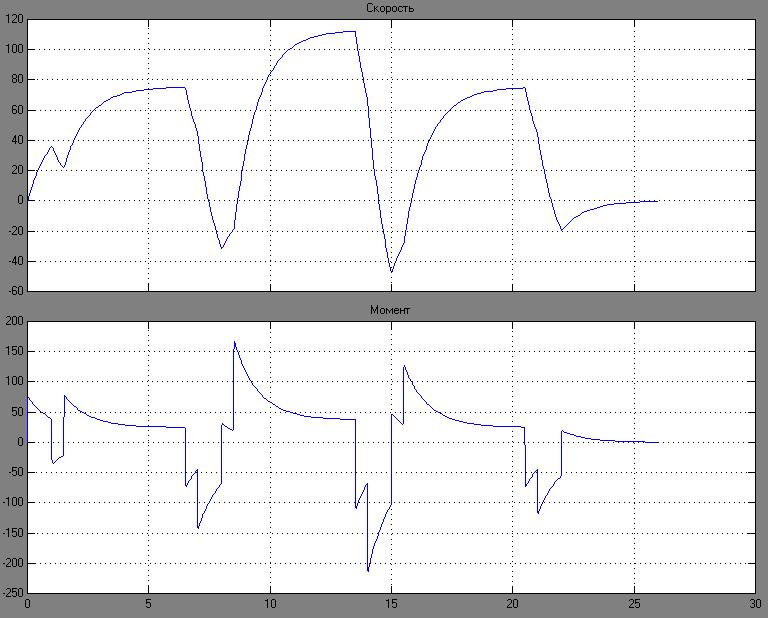
Рис. 3 Диаграмма скоростей и моментов для ДТП НВ

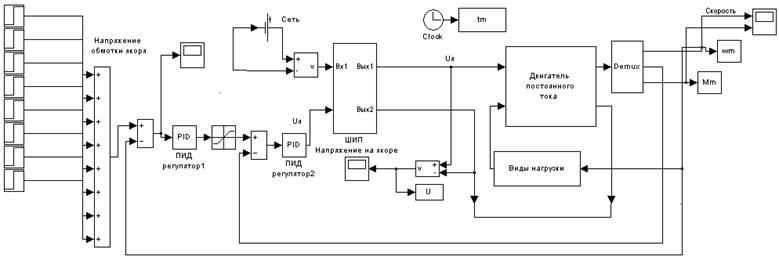
Рис. 4. Виртуальная модель замкнутой системы и ШИП

Настройка ПИД регуляторов

В системах подчинённого регулирования используются регуляторы четырёх типов:

- пропорциональные (П) с передаточной функцией ;

- интегральные (И), ;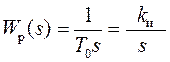

- пропорционально-интегральные (ПИ), ;

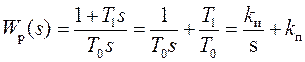- пропорционально-интегро-дифференциальные (ПИД),

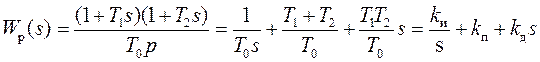Последовательность синтеза регуляторов в подчиненных системах электропривода следующая.

Для первого контура результирующее эквивалентное звено, состоящее из исходного звена с передаточной функцией и регулятора с передаточной функцией , всегда можно привести к интегрирующему звену с передаточной функцией 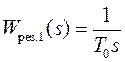. Следовательно, регулятор всегда должен быть построен так, чтобы

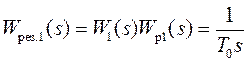Если в основной цепи имеется интегрирующее звено 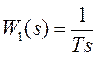, то регулятор должен быть пропорциональным, причём

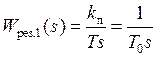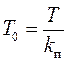; , где ; при постоянная времени может иметь любое малое значение. После создания замкнутого контура, его передаточная функция будет соответствовать апериодическому звену с малой постоянной времени .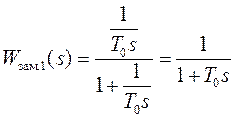

Если исходное звено является апериодическим с передаточной функцией 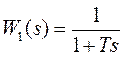, то регулятор должен иметь передаточную функцию, соответствующую ПИ-регулятору, .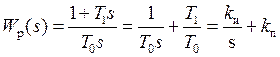

Тогда 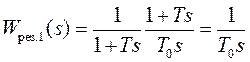, или после охвата обратной связью опять получим: .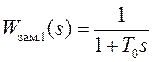

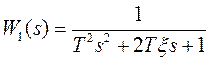Если исходная система представляет собой колебательное звено с передаточной функцией , то в соответствии с изложенным подходом регулятор должен быть ПИД-регулятором с передаточной функцией .

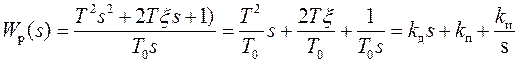В этом случае передаточные функции разомкнутой и замкнутой системы примут вид: .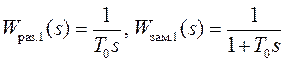

Рассмотрим второй контур. Если исходное звено второго контура является интегрирующим с передаточной функцией 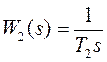, то общая передаточная функция первого и исходного второго звена будет равна: 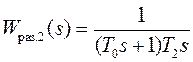. Для таких и более сложных систем регулятор синтезируется таким образом, чтобы в замкнутом контуре получить желаемую передаточную функцию. В качестве желаемых передаточных функций в системах электропривода используются две: