Стабилизация двухмассовой системы: модальный метод синтеза с использованием полиномиального разложения. Решение матричного полиномиального диофантова уравнения

Научный вестник НГТУ. – 2010. – № 1(38)

УДК 681.513

Стабилизация двухмассовой системы: модальный метод синтеза с использованием полиномиального разложения*

А.А. ВОЕВОДА

На примере решения задачи стабилизации двухмассовой системы, рассматриваемой как двухканальной с дополнительным требованием астатизма, показаны возможности использования полиномиального представления описаний объекта и регулятора. Задача синтеза сведена к решению матричного полиномиального диофантова уравнения.

Ключевые слова: модальный синтез, полиномиальное разложение, регулятор, астатизм, наблюдатель, двухмассовая система

Введение

При синтезе многоканальных систем управления широкое распространение нашли модальные методы синтеза, базирующиеся на описании уравнений объекта и регулятора в пространстве состояний. При этом широко используются наблюдатели состояния. При наложении дополнительных условий, например таких, как астатизм, возникают дополнительные трудности. Не так широко распространено конкурирующее направление, в котором используется полиномиальное (матричное) разложение. При синтезе одноканальных систем модальным методом с использованием полиномов задача сильно упрощается. Пример синтеза регулятора, решающего задачу стабилизации двухмассовой системы приведен в [1], а как двухканальной – в [2]. В обоих примерах не требуется введение наблюдателя и нет необходимости решать вопрос о переходе к специального вида базисам. Для сравнения в [3] исследован вопрос синтеза регулятора, стабилизирующего двухмассовую систему классическим модальным методом с использованием наблюдателей полного и пониженного порядка без требования астатизма. К недостаткам классического подхода можно отнести то, что регулятор находится в обратной связи.

1. Постановка задачи

В качестве объекта управления возьмем двухмассовую систему [1–3]. Предполагается два управляющих сигнала – силы –  и , приложенные к массам  и : модель объекта представляет собой систему из двух грузов, подвешенных последовательно на двух пружинах жесткости  и  с коэффициентами демпфирования  и . Управляемые величины – координаты грузов  и , отсчитываемые от состояния равновесия. Выпишем модель объекта управления:

,                                             (1)

.

Поставим задачу автономизации каналов с заданными полюсами у замкнутой системы. В качестве исполнительных органов используем интеграторы.

Синтез регулятора. С учетом интеграторов

,                                                                   (2)

«модифицированный» объект (1), (2)  описывается системой уравнений

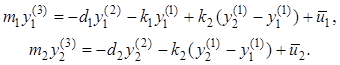                                     (3)

Перейдем в (3) к полиномиальному описанию:

.

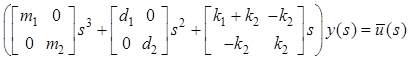Здесь и . Обозначим матрицы при , и  через ,  и . Тогда описание модифицированного объекта (далее «объекта») примет вид , где . В общем случае это соответствует левому матричному полиномиальному описанию , где  – матричная передаточная функция модифицированного объекта. В нашем случае  – единичная матрица размером 2 на 2.

Выберем структуру системы управления вида «задание–сигнал рассогласования–регулятор–объект–обратная связь». Опишем систему уравнениями

,   ,   , откуда найдем передаточную функцию системы

.

Воспользовавшись известными матричными преобразованиями [2], получим описание передаточной функции замкнутой системы в виде

.                                                 (4)

Варианты полиномиального разложения. В зависимости от выбора правого/левого описания для объекта и регулятора возможны четыре случая. Выберем правое разложение для объекта и левое разложение для регулятора:

,    .                                       (5)

Найдем связь между входом  и выходом – подставим (5) в (4):

.                                        (6)

Нашли передаточную функцию системы и, следовательно, ее «знаменатель» – . Таким образом, при известном правом представлении объекта в предположении, что ищем регулятор в виде левого разложения, задача синтеза сводится к решению диофантова уравнения

.                                                    (7)

Здесь  – характеристическая матрица системы размером 2 на 2.

Синтез.Воспользуемся представлением объекта и регулятора (5), что приводит