Синтез многоканальных систем. Частное решение однородного уравнения, индекс наблюдаемости, синтез правильного компенсатора, решение диофантова уравнения, параметризация решения, условия разрешимости, процедура синтеза

7.  СИНТЕЗ МНОГОКАНАЛЬНЫХ СИСТЕМ

Частное решение однородного уравнения, индекс наблюдаемости, синтез правильного компенсатора, решение диофантова уравнения, параметризация решения, условия разрешимости, процедура синтеза.

Для системы общего вида $39 задача синтеза S138 сводится по существу, к решению обобщенного тождества Безу S139. На базе свойств, приведенных в S139, S140, получена процедура синтеза S142. При первом чтении можно опустить доказательства из S139, S140, S141.

$39.  Рассмотрим систему

                                                                                                                  

С

P

                                                                                                         

               

-

 

Система å

Здесь размерность входа объекта  равна  и размерность выхода объекта  равна . Опишем систему å аналогично тому, как это сделано в $26: введем вектор . Тогда , где

, ,

, .

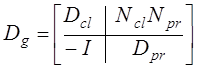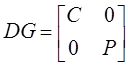Информацию о матрице D можно получить в S117. Осталось описать матрицу F ($26): . Но , . Следовательно,

.

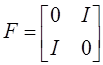Найдем характеристический полином S112:

.

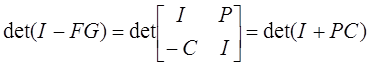Из S113 вычислим . Несложно найти  (см. ниже матрицу ). Тогда, учитывая, что  и , получим передаточную функцию по каналу “первый вход – второй выход”:  . Из уравнения замкнутой системы S119 найдем характеристический полином: . Но из (а) S119:

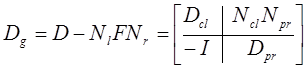, следовательно,

.

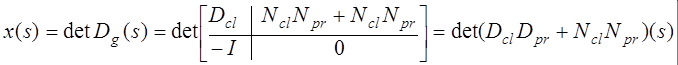Можно показать, что

.

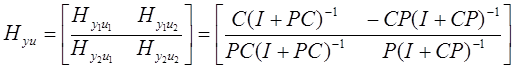S138.  Сформулируем задачу синтеза. Пусть дан объект , для которого внутренне правильное правое взаимно простое разложение . Если вспомнить матрицы в уравнениях псевдосостояния , то кратко можно объект записать так: . Здесь  - столбцово приведенное; столбцовые степени равны . Матрица коэффициентов при высших степенях .

Найти регулятор, или чаще говорят компенсатор (compensator), С такой, что  (кратко записывается так: , вектор псевдосостояния ). Здесь  - внутренне правильное левое взаимно простое разложение. Причем матрица  - столбцово приведенная. Необходимо найти такой компенсатор С, чтобы система å была экспоненциально устойчивой и имела заданный (предписанный) характеристический полином .

П о я с н е н и я.

1. Внутренне правильное правое взаимно простое разложение всегда можно получить из произвольного правого разложения. Для этого надо при помощи элементарных операций выделить наибольший общий правый делитель и сделать  столбцово приведенной.

2. Предположение, что матрица  столбцово приведенная, равносильно тому, что

, где  - биправильная и .

3. Добиться  можно “перестановкой” (перенумерацией) входов объекта:

, где введено обозначение , . У матрицы  матрица старших коэффициентов равна единичной матрице.

4. Система å удовлетворяет условиям ХУ, ХУМПО, ВС. Поэтому

å экспоненц. уст..

И с с л е д у е м  å. Характеристический полином

.

Передаточная функция :

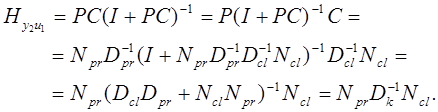
Здесь введено обозначение . Получили

.

Кроме того, имеем , . Система в целом же описывается:

, где , , ,

.

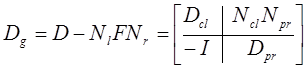При нулевом входе динамические процессы в системе описываются

.

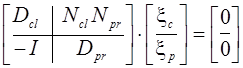Вторую строку умножим на  и прибавим к первой :

.

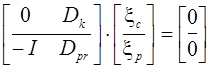Это равносильно

, .

В ы в о д ы.

1. Матрица  полностью определяет псевдосостояние  системы å при нулевом входе.

2.  “управляет” непосредственно динамикой псевдовектора состояния объекта  при нулевом входе.

3. Если матрица  диагональная, то нет связей между  и .

К о м м е н т а р и й. Можно считать, что  даны и удовлетворяют условиям S138. Матрицу  выбираем такую, чтобы . Поиск компенсатора сводится к решению уравнения . Решение уравнения ,  должно быть внутренне правильным и матрица Х столбцово приведенной. При решении этой задачи можно использовать обобщенное уравнение Безу.

S139.  Рассмотрим уравнение

,                                                    (а)

где матрицы  и  описывают объект  и удовлетворяют условиям S138. Матрицы ,  являются решение уравнения (а) тогда и только тогда, когда существует  такое, что

, .                                 (б)

Здесь  - элементы обобщенного тождества Безу:

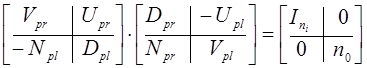 .                                  (в)

Кроме того,  - взаимно простые слева тогда и только тогда, когда  взаимно простые слева.

К о м м е н т а р и и.

1. Пусть нашли , полагаем тогда , т.е. . При этом хотелось бы, чтобы  были внутренне правильными и взаимно простыми слева, а матрица Х - строчно приведенной.

2. Решение  уравнения (а) параметризовано матрицей  (б), которое определяет  единственным образом. Из уравнения (б) следует, что  . Следовательно, можно считать, что  - это частное от деления  на . Здесь  остаток, т.е. .