Синтез многоканальных систем. Частное решение однородного уравнения, индекс наблюдаемости, синтез правильного компенсатора, решение диофантова уравнения, параметризация решения, условия разрешимости, процедура синтеза, страница 2

Д о к а з а т е л ь с т в о. Пусть существует такое , что  вычислены по (б) и матрицы  - элементы (в). Покажем, что такая пара матриц  удовлетворяет (а). Подставим (б) в левую часть (а) и перегруппируем члены:

.

Проанализируем выражения в скобках. Из (в) найдем элементы матрицы произведения, стоящие в первой строке и первом столбце, а также во второй строке и первом столбце:

, -.

Вернемся к предыдущим вычислениям. Теперь очевидно, что в правой части осталось . Доказали, что , выбранные по (б), удовлетворяют (а).

Пусть  - решение (а). Покажем, что оно имеет вид (б). Из произведения левой части (в) найдем элемент (1, 1): . Умножим его слева на : . Введем обозначения: , . Из предыдущего уравнения получили , т.е.  - частное решение (particular solution) уравнения (а). Возьмем уравнение (а) и перейдем к однородному уравнению (homogeneous equation):

.                                                       (г)

Пусть  - какое-нибудь решение однородного уравнения (г) (полиномиальное!). Подставим его в (г): . Из уравнения (в) для элемента (2, 1) имеем , откуда

.                                                     (д)

Продолжим наши вычисления:

.

Последнее равенство получили в результате введения новой матрицы:

.                                                           (е)

Таким образом, получили общее решение однородного уравнения (г):

, .                                           (ж)

Второе уравнение непосредственно следует из (е).

Покажем, что решение (ж) – полиномиальное. Для этого достаточно показать, что  (е) полиномиальное. Воспользуемся элементом (2, 2) из (в):  . Умножим его слева на :

В последнем равенстве использованы формулы (ж).

Получены частное решение  неоднородного уравнения и общее решение  однородного уравнения. Доказали, что решение уравнения (а) имеет вид (б).

Его можно записать так:

.

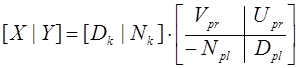Правая матрица – это унимодальная матрица, так как ее обратная матрица также полиномиальная (в). Следовательно,

 .

Доказали последнее утверждение: матрицы  взаимно простые слева тогда и только тогда, когда матрицы  взаимно простые слева.

S140.  Пусть для объекта  дано внутренне правильное взаимно простое разложение , где  - невырожденная столбцово приведенная матрица, столбцовые степени которой равны  и матрица коэффициентов при высших столбцовых степенях равна единичной . Справедливо следующее утверждение:

 и 3).

Утверждения 1), 2), 3) даны ниже:

1)  уравнение компенсатора

                                                     (а)

имеет решение  такое, что  и  и  левое разложение внутренне правильное, Х – столбцово приведенная и внутренне правильная со столбцовыми степенями равными ,  - коэффициентная матрица при высших столбцовых степенях;

2)   - приведенная по строчкам и столбцам;  - степени строк;  - степени столбцов. Здесь , .

Данное утверждение эквивалентно следующему:

,                                      (б)

где  - биправильная, причем ;

3)  для заданного  решение  уравнения (а) удовлетворяет условию

 .                                                  (в)

П р и м е ч а н и е. Если выполнены условия 2) и 3), то

,                                                         (г)

причем если , , .

Д о к а з а т е л ь с т в о. Докажем, что из 1) следует 2) и 3). Учтем, что:  - внутренне правильное правое взаимно простое разложение:  - приведенная по столбцам матрица; Р – строго правильная матрица. Отсюда следует справедливость равенств

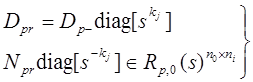,                                            (д)

где  - биправильная и

.                                                       (е)

Так как  левое внутренне правильное разложение, то , можем рассуждать так же, как и при рассмотрении объекта, т.е. при написании соотношений (д):

, .                                 (ж)

Здесь  - биправильная, т.е.

.                                                           (з)

Из (ж) и (д) следует (б) (подставим первое уравнение из (д) и первое уравнение из (ж) в первый член уравнения (а)):

.

Несложно получить

.

Как мы знаем, матрицы, стоящие в круглых скобках, биправильные. Поэтому выражение в правой части, которое обозначим через

 -                                            (к)

биправильное. Обозначим . Так как

, то

.                                            (л)

Из (ж) (второе уравнение) следует (в). Наконец, (л) – это (г).

Докажем, что из 2) и 3) следует 1). Отметим прежде всего, что (д), (е) и в этом случае справедливы, а (в) влечет (ж) (второе уравнение). Нам нужно показать, что подстановка Х и , удовлетворяющих условиям 2) и 3), в левую часть уравнения (а) удовлетворяет этому уравнению. Подставим первое уравнение из (д) и уравнение (б) в (а):