Синтез многоканальных систем. Частное решение однородного уравнения, индекс наблюдаемости, синтез правильного компенсатора, решение диофантова уравнения, параметризация решения, условия разрешимости, процедура синтеза, страница 3

.

Преобразуем это уравнение:

.

Обозначим левую часть через : . Тогда имеем

.

Рассмотрим правую часть:  - биправильная матрица,  - правильная матрица (вторая формула из (ж)),  - строго правильная (вторая формула в (д)), наконец  - биправильная матрица. Так как в фигурных скобках матрица правильная и  биправильная, то и  биправильная.

Можем записать, что

,                                                     (м)

где  - биправильная. Значит, Х строчно приведенная, ее строчные степени равны  и . Из (ж) (второе уравнение) следует, что  - правильное. Из (м) получаем

, что  - правильное (ж), тогда . Доказательство окончено.

S141.  Пусть для объекта  дано внутренне правильное правое взаимно простое разложение , где  - невырожденная столбцово приведенная матрица, столбцовые степени которой равны  и матрица коэффициентов при высших столбцовых степенях равна единичной . Кроме того, задано внутренне правильное левое взаимно простое разложение , где  - невырожденная строчно приведенная по строчкам матрица. Задана матрица .

1)  Пусть:

i)    - приведенная по строчкам и столбцам со строчными степенями  и столбцовыми степенями ,

ii)  пусть

 ,                                                         (а)

где   (m - максимальная степень элементов матрицы ).

2)  Уравнение  имеет решение Х и  такое, что  - левое разложение – внутренне правильное, матрица Х – приведенная по строчкам и имеет строчную степень .

Утверждается, что из 1) следует 2).

П р и м е ч а н и я.

1. m - это индекс наблюдаемости (observability index of the plant P). Пусть  - минимальная реализация объекта Р. Тогда m - это наименьшее целое l такое, что

, т.е. m-1 – это наименьшее число производных выхода, необходимых для восстановления состояния в момент .

2. Для реализации компенсатора надо задавать  так, чтобы выполнялись i), ii). Другими словами,

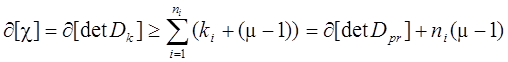, где  - число входов.

3. По-видимому, оценка (а) довольно грубая.

Д о к а з а т е л ь с т в о. Пусть задано  такое, что выполнены условия i), ii). Тогда решение  уравнения  в соответствии с (б) из S139 может быть записано так:

, .

Посмотрим на  как на результат деления  на : . Другими словами,. Следовательно, . Отсюда  . Наконец,

.

Кроме того, что   и  т.е. . Условия (а) S140 выполнены, следовательно, существует решение  такое, что Х,  полиномиальные,  левое разложение внутренне правильное, Х – приведенная по строчкам и строчные степени ее равны .

S142.  Подведем итоги. Решение  уравнения  обозначим , т.е. .

Существует компенсатор , где  - решение  уравнения  тогда и только тогда, когда:

1)  ,  ( - предписанный характеристический полином системы å);

2)   - приведенная по строчкам и столбцам, строчные степени - , столбцовые степени - ; Матрица  определяет : ;

3)  для всех i .

К о м м е н т а р и и.

1.  делит  справа.

2. Х задано посредством .

3. , .

4. Для простоты полагают, что  имеет  различных собственных значений  при  собственных векторах:

 .

Отсюда доказывается, что первый комментарий равносилен  = для  и 3) равносильно ,  - числовая матрица и

.

ОСНОВНЫЕ ТЕРМИНЫ

Биправильная матрица (biproper matrix)

Вектор состояния (state space vector)

Внутренне правильный (internally proper)

Взаимно простые справа (right-coprime)

Взаимно простые слева (lrft-coprime)

Взаимосвязанная система (interconnected system)

Входной развязанный нуль (input-decoupling zero)

Выходной развязанный нуль (output-decoupling zero)

Детерминантный делитель (determinant deviser)

Достижимый (reachable)

Желаемая область (desirable)

Инвертируемый (invertible)

Инвариантный полином (invariant polynomial)

Индекс наблюдаемости (onservability index)

Индекс управляемости (controllability index)

Коэффициентная матрица при высших степенях (highest degree coeffisient matrix)

Класс сигналов

Компенсатор (compensator)

Компенсатор в обратной связи (feedback compensator)

Левое взаимно простое разложение матрицы (left coprime fraction)

Левое-правое взаимно простое разложение H (left-right-coprime fraction)

Левоэквивалентный (left equivalent)

Левое матричное разложение (left matrix fraction)

Левый делитель (left divisor)

Левый общий делитель матриц (common left divisor)

Левая элементарная матрица (left elementery matrix)

Матрица системы (system matrix)

Матрица системы в пространстве состояний (state-space system matrix)

Матрицы Теплица (Toeplitz matrix)

Матричная передаточная функция (transfer functoin matrix)

Минимальная реализация (minimal relizatoin)