Примеры. Другие задачи синтеза. Пример реализации компенсатора. Асимптотическое отслеживание, компенсация возмущений и развязывание. Точная реализация модели

6. Примеры. Другие задачи синтеза

Продолжим изучение задачи синтеза. Вначале приведем расчета устройства управления для двухканального объекта посредством двух алгоритмов, изученных в разделе втором. Далее коснемся задач асимптотического отслеживания, компенсации возмущений, развязывания и точной реализации модели. Закончим курс примером синтеза правильного компенсатора минимального порядка.

6.1. Пример реализации компенсатора

Проиллюстрируем применение реализаций 1 и 2, приведенный в пятом разделе.

Пример 6.1. Рассмотрим объект

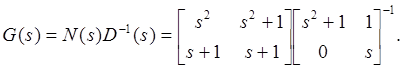
Вычислим

, .

Сейчас мы сможем разложить  как

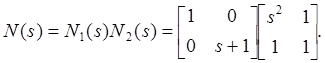
Вычислим

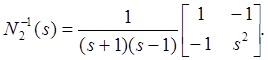
Следовательно, мы получим:

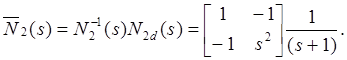
Сейчас мы выберем  с  где  гурвицевы полиномы минимальной степени, таких, что  правильная. Вычислим

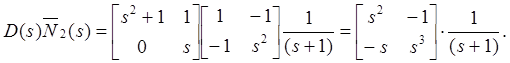
Следовательно, мы можем выбрать

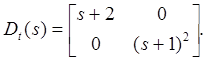                                                     (6.1)

Реализация  обеспечит развязывание системы с передаточной матрицей

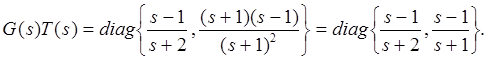                    (6.2)

Реализация 1. Реализуем  по схеме рис.5.4. Вычислим

  

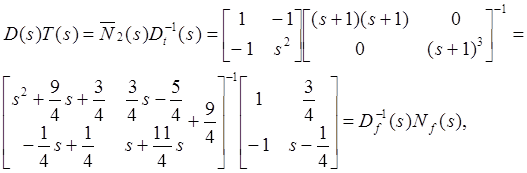
   где  и  взаимно простые слева. Строчный индекс оказался равным . Очевидно, что  и выбирая  произвольно, например,

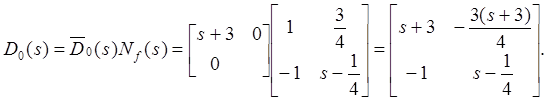
которая имеет строчные степени все равные единице m=1 и является строчно приведенной. Ясно, что  следовательно, мы имеем . Вычислим

.

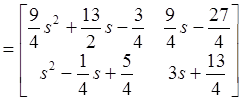Таким образом,  и  в (5.46), (5.47) могут быть найдены из

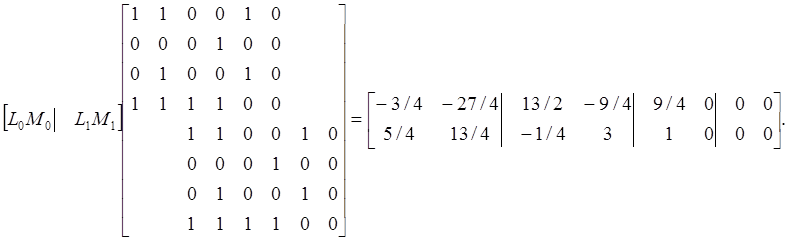
Получаем

                           

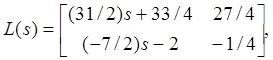
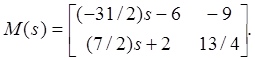
Этим завершается первая реализация.

Реализация 2. Реализуем  по схеме рис.5.7. Мы имеем  и , следовательно,  и . Выберем  и

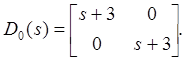
Ввиду того, что , выбираем  произвольно, например, равным  (степени 1). Ввиду , полагаем . Отсюда получили

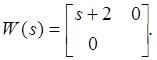
Очевидно, что  полагаем  и

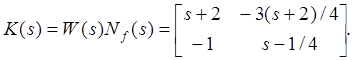
Матрицы  и  могут быть найдены из (5.61)

                          

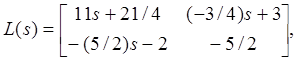
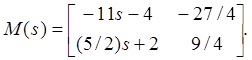
Этим закончена вторая реализация.

В этом примере общие степени компенсаторов одинаковы и равны двум. В общем случае степень компенсатора во второй реализации не превышает степени второй реализации.

Вместо развязывания объекта по каждой паре вход-выход можем развязывать группы входов0выходов. В этом случае объект будет развязан в соответствии с блочно-диагональной матрицей.

6.2. Асимптотическое отслеживание, компенсация возмущений и развязывание

В отечественной литературе термины, приведенные в заголовке, нечетко определены и часто трактуются неоднозначно. Для исключения неоднозначности приведем их английский эквивалент – asymptotic tracking, disturbance rejection and decoupling. В этой части мы спроектируем робастную системы, обеспечивающую развязывание, асимптотическое отслеживание и компенсацию возмущений. Пусть  будет p*p несингулярная правильная рациональная матрица. Ее каналы могут быть развязаны без использования сокращения неустойчивых полюсов и нулей

где  единственным образом определяется из , и степени  должны быть выбраны из условия правильности разомкнутого компенсатора . Если объект должен быть лишь развязан, полиномы  назначаем произвольно. Если при синтезе требуется не только развязывание, но и дополнительно отслеживание и компенсация возмущений, полиномы  не могут быть произвольно назначены. Они должны стабилизировать обратную связь и дополнительно обеспечивать отслеживание и компенсацию возмущений.

С целью достичь асимптотическое отслеживание и компенсацию возмущений, а также иметь свойство робастности к параметрическим возмущениям, мы введем, как обсуждалось ранее (п.4.5), внутреннюю модель , как показано на рис.6.1.

 

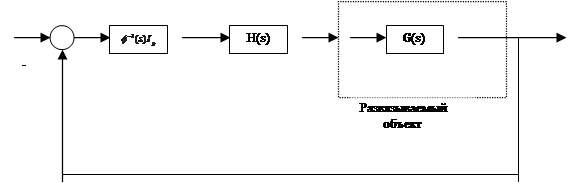
Рис.6.1. Синтез робастной системы

Если мы введем диагональную полиномиальную матрицу

с  правильными или строго правильными, тогда на рис.6.1 приводится к p отдельным одноканальным системам с обратными единичными связями, в прямой цепи которых стоят последовательно слева направо . Передаточная функция такой системы, очевидно, равна

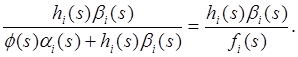                                       (6.3)

Их знаменатели есть полиномы степени  Если мы требуем, чтобы  были строго правильными, тогда  есть число свободных параметров в ;  есть число свободных параметров в. Следовательно, если  и  взаимно простые, корни  в (6.3) могут быть произвольно назначены правильным выбором  и . Условие  асимптотической устойчивости, отслеживания и компенсации возмущений состоит в том, что у  нет корней, являющихся передаточными нулями  или ввиду того, что  и  квадратные, не являются корнями . Так как  есть множитель , мы заключаем, что если ни один корень  не является передаточным нулем , то  и  взаимно простые и корни  могут быть произвольно назначены. По назначенным  мы можем вычислить  и . Далее синтезируем систему с обратной связью типа вход-выход, которая должна развязать объект так: