Рассмотрим
![]() .
(6.6)
.
(6.6)
Мы утверждаем, что если ![]() полного строчного ранга в
полного строчного ранга в ![]() , тогда
, тогда ![]() правильная,
если и только если
правильная,
если и только если
![]() (6.7)
(6.7)
где ![]() обозначает
степень i-й строки. Если
обозначает
степень i-й строки. Если ![]() квадратная,
это утверждение, по существу, совпадает с теоремой 2.11.
квадратная,
это утверждение, по существу, совпадает с теоремой 2.11.
Условие правильности в
(6.7) не дает нам подсказки как находить ![]() минимальной
степени. Ниже мы дадим такой метод. Пусть
минимальной
степени. Ниже мы дадим такой метод. Пусть ![]() . Тогда
(6.5) преобразуется в
. Тогда
(6.5) преобразуется в ![]() или
или
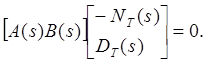 (6.8)
(6.8)
Это полиномиальное
уравнение изучается во втором разделе; следовательно, все результаты,
обсуждаемые во второй части, могут быть непосредственно применены. Пусть ![]() обозначает правое ядро (ненулевое
пространство) (6.8). Его размерность, согласно известной теореме,
обозначает правое ядро (ненулевое
пространство) (6.8). Его размерность, согласно известной теореме,
![]()
Сейчас мы можем применить
теорему 2.16 для решения (6.8). Сформируем обобщенный результант ![]() из коэффициентов матриц
из коэффициентов матриц ![]() и
и ![]() в соответствии с теоремой 2.16. Затем
исследуем линейную зависимость столбцов в направлении слева направо, используя
столбцовый поисковый алгоритм. Здесь будет в точности
в соответствии с теоремой 2.16. Затем
исследуем линейную зависимость столбцов в направлении слева направо, используя
столбцовый поисковый алгоритм. Здесь будет в точности ![]() первично
зависимых столбцов в
первично
зависимых столбцов в ![]() .
Пусть
.
Пусть ![]() полиномиальная матрица
полиномиальная матрица ![]() будет решением, соответствующим этим
будет решением, соответствующим этим ![]() первично зависимым столбцам. Тогда
первично зависимым столбцам. Тогда ![]() в соответствии с теоремой, двойственной
теореме 2.16, столбцово неприводимая и столбцово приводимая, и является
минимальным полиномиальным базисом правого ядра (6.8).
в соответствии с теоремой, двойственной
теореме 2.16, столбцово неприводимая и столбцово приводимая, и является
минимальным полиномиальным базисом правого ядра (6.8).
Пусть
![]() - столбцово степенная коэффициентная
матрица
- столбцово степенная коэффициентная
матрица ![]() . Для удобства обсуждения мы положим
. Для удобства обсуждения мы положим ![]() и разобьем
и разобьем ![]() и
и ![]() :
:
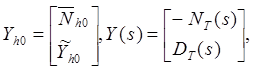 (6.9)
(6.9)
где ![]() и
и
![]() p*r и
p*r и ![]() и
и ![]() r*r
матрицы. Отметим, что ввиду положения правильности
r*r
матрицы. Отметим, что ввиду положения правильности ![]() ,
матрица
,
матрица ![]() в соответствии стеоремой 2.16 всегда
правильная, так что
в соответствии стеоремой 2.16 всегда
правильная, так что ![]() и
и ![]() столбцово
приведенная или
столбцово
приведенная или ![]() полного столбцового ранга. В
задаче минимального синтеза
полного столбцового ранга. В
задаче минимального синтеза ![]() в (6.8) необязательно
квадратная и
в (6.8) необязательно
квадратная и ![]() может быть не определена; следовательно,
нет гарантии, что
может быть не определена; следовательно,
нет гарантии, что ![]() - столбцово степенная
коэффициентная матрица
- столбцово степенная
коэффициентная матрица ![]() (6.9), полного столбцового
ранга. Отметим, что
(6.9), полного столбцового
ранга. Отметим, что ![]() имеет, как следует из
столбцового поискового алгоритма, неполный столбцовый ранг.
имеет, как следует из
столбцового поискового алгоритма, неполный столбцовый ранг.
Теорема 6.1. Если ![]() в (6.9) минимальный полиномиальный базис
(6.8), полученный по теореме 2.16, то
в (6.9) минимальный полиномиальный базис
(6.8), полученный по теореме 2.16, то ![]() правильная,
если и только если
правильная,
если и только если ![]() ранга r.
ранга r.
В
этой теореме условие полного столбцового ранга ![]() или то,
что
или то,
что ![]() минимальный базис существенно; в противном
случае теорема не имеет места. Теорема соответствует случаю, когда
минимальный базис существенно; в противном
случае теорема не имеет места. Теорема соответствует случаю, когда ![]() . Обсудим сейчас общий случай. Если
. Обсудим сейчас общий случай. Если ![]() , очевидно, что решения
, очевидно, что решения ![]() уравнения (6.4), правильного или
неправильного, нет. Если
уравнения (6.4), правильного или
неправильного, нет. Если![]() матрицы
матрицы ![]() и
и ![]() размера
размера
![]() имеют ранг
имеют ранг ![]() и
теорема 6.1 еще имеет место. В этом случае, с целью получить минимальной
решение, упорядочим
и
теорема 6.1 еще имеет место. В этом случае, с целью получить минимальной
решение, упорядочим ![]() по возрастанию степеней
столбцов, так что
по возрастанию степеней
столбцов, так что ![]() Тогда первые r
столбцов при несингулярной
Тогда первые r
столбцов при несингулярной ![]() дают минимальное
правильное решение (6.4). На этом завершим обсуждение задачи минимального
синтеза.
дают минимальное
правильное решение (6.4). На этом завершим обсуждение задачи минимального
синтеза.
6.4. Еще один пример синтеза
Ниже приведем пример минимального синтеза.
Пример 4. Найдем минимальное правильное решение
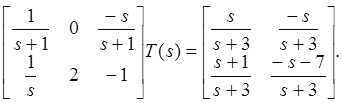
Умножив на ![]() и подставив
и подставив ![]() ,
получим
,
получим

Ясно, что ![]() . В соответствии с теоремой, двойственной
теореме 2.16, сформируем
. В соответствии с теоремой, двойственной
теореме 2.16, сформируем ![]() и применим столбцовый
поисковый алгоритм.
и применим столбцовый
поисковый алгоритм.
Найдем:
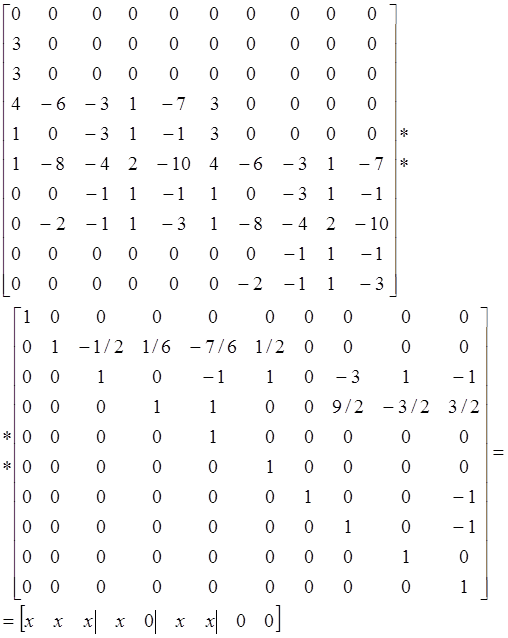
Здесь x
обозначает ненулевые столбики и 0 нулевые столбики. Обозначение « ![]() » объяснено во втором разделе. В матрице
» объяснено во втором разделе. В матрице ![]() четыре линейно независимых столбца. Три из
них первично зависимые столбцы помечены стрелками. Отметим, что по теореме 2.16
линейно независимые столбцы могут появиться только как в
четыре линейно независимых столбца. Три из
них первично зависимые столбцы помечены стрелками. Отметим, что по теореме 2.16
линейно независимые столбцы могут появиться только как в ![]() -столбцах, так и в
-столбцах, так и в ![]() -столбцах,
как показано в этом примере. По трем первично зависимым столбцам, используя
дуальную формулу к (1.9), вычислим:
-столбцах,
как показано в этом примере. По трем первично зависимым столбцам, используя
дуальную формулу к (1.9), вычислим:
|
|
|

что приводит немедленно к
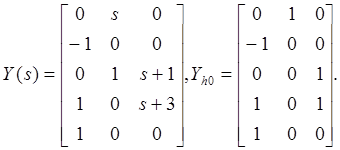
![]() имеет
ранг 3 для каждого
имеет
ранг 3 для каждого ![]() из
из ![]() , т.е.
она столбцово неприводима. К тому же она столбцово приведенная и
, т.е.
она столбцово неприводима. К тому же она столбцово приведенная и ![]() имеет полный столбцовый ранг.
Следовательно,
имеет полный столбцовый ранг.
Следовательно, ![]() - минимальный полиномиальный
базис для правого нулевого пространства (ядра). Первый и третий столбцы
- минимальный полиномиальный
базис для правого нулевого пространства (ядра). Первый и третий столбцы ![]() образуют
образуют ![]() ранга
2; тогда мы имеем:
ранга
2; тогда мы имеем:
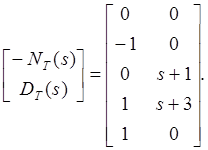
Матрица ![]() и
и ![]() найдены.
Приступаем к вычислению неизвестной матрицы
найдены.
Приступаем к вычислению неизвестной матрицы ![]() :
:

Это минимальное правильное решение.
Основные термины
Асимптотическое отслеживание (asymptotic tracking), п.4.5
Блокирующий нуль (blocking zero), п.3.4
Ведущий коэффициент (leading coefficient), п.2.1
Ведущий элемент (pivot element), п.1.4
Верхняя форма Гейзенберга (upper Hessenberg form), п.1.5
Взаимно простой (coprime), п.2.1
Взаимно простой справа (right coprime), п.1.2
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.