Примеры. Другие задачи синтеза. Пример реализации компенсатора. Асимптотическое отслеживание, компенсация возмущений и развязывание. Точная реализация модели, страница 2

Результирующая система асимптотически устойчива и развязанная. Она еще должна асимптотически отслеживать заданный вход и компенсировать внутренние возмущения на объект. При таком синтезе, если имеют место параметрические возмущения в объекте и компенсаторе (исключая внутреннюю модель), свойство асимптотического отслеживания и компенсации возмущений сохраняется.

Пример 6.2. Рассмотрим пример 2.1. Мы имеем , , ,  . Предположим, задача синтеза состоит в том, что объект должен отслеживать входную ступеньку  и компенсировать внутренние возмущения объекта в форме , тогда мы имеем . Так как  и  взаимно простые,  и  могут быть найдены такими, чтобы стабилизировать систему рис.6.1. Совершенно произвольно выберем . Тогда решение

есть  Если , решение

есть 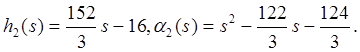 Далее мы заменим (6.1) и (6.2) на

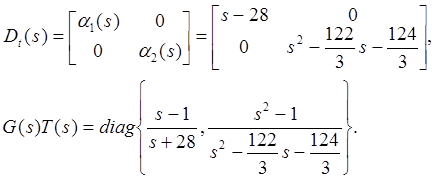
Сейчас  реализована как система с обратной связью типа вход-выход и представлена внутри прямоугольника на рис.6.1. Синтез завершен. Эта часть синтеза похожа на расчеты в примере 6.1 и здесь не приведена.

6.3. Точная реализация модели

Задачи синтеза, обсуждавшиеся перед этим, касались лишь назначения полюсов знаменателя; числитель матрицы оставался без уточнения. В этом подразделе мы обсудим назначение матрицы – знаменателя одновременно с назначением матрицы числителя, или эквивалентно в целом всей части передаточной матрицы. Эта задача называется часто задачей точной реализации модели (exact model matching problem).

Рассмотрим объект с q*p правильной рациональной матрицей . Желаемая модель предполагается вида q*r правильной рациональной матрицы . Проблема состоит в поиске такой конфигурации компенсатора, чтобы вся результирующая система имела  в качестве ее передаточной матрицы. Мы будем изучать проблему, используя разомкнутый компенсатор, такой что

.                                                         (6.4)

В данном случае, если решение  уравнения (6.4) существует и является правильной рациональной матрицей, тогда синтез может быть выполнен и реализация  осуществима в системе рис.5.4 или рис.5.7 с обратной связью типа вход-выход. Таким образом, задача синтеза сконцентрирована  на решении (6.4).

Пусть  и  будут i-ми столбцами  и . Тогда (6.4) может быть переписано как  при . Каждое уравнение  есть линейное алгебраическое уравнение с элементами в  - поле вещественных рациональных функций. Следовательно, теорема о существовании решения линейной системы уравнений может быть применена непосредственно. Отсюда необходимое и достаточное условие  существования  решения  уравнения (6.4)

над . В общем случае решение  представляет собой правильную или неправильную рациональную матрицу. В задаче точного представления модели будем интересоваться только решениями, которые представляют собой правильные рациональные матрицы. Кроме того, мы потребуем, чтобы степень  была как можно меньше. Такая задача поиска правильной  с минимальной степенью и удовлетворяющая (6.4) называется задачей минимального синтеза (minimal dasign problem).

Перед тем, как продвигаться дальше, мы введем некоторые понятия. Напомним, что  и  взаимно простые слева, если и только если их наибольший общий делитель есть унимодальная матрица, т.е. если  некоторый множитель

, то эта матрица унимодальная. В соответствии с этим мы можем определить q*n полиномиальную матрицу  с , как строчно неприводимую (row irreducible), если  в любом разложении  унимодальная. В соответствии с теоремой 2.9  строчно неприводима, если и только если  для всех и .

Мы можем также расширить концепцию строчной неприводимости на неквадратные матрицы. Квадратная полиномиальная матрица  строчно приведена, если  равна сумме степеней . Это определение влечет, что  строчно приведена, если и только если ее строчно степенная коэффициентная матрица невырождена. В соответствии с этим, мы определим q*n полиномиальную матрицу  полного строчного ранга , то существует унимодальная полиномиальная матрица , такая, что  строчно приведенная. Мы можем аналогично определить столбцовую неприводимость и столбцовую приводимость для неквадратных полиномиальных матриц. После этого введения мы готовы к изучению задачи минимального синтеза.

Прежде всего обсудим условие правильности решения  уравнения  (6.4). Если  квадратная и несингулярная, ответ очень простой:  правильная, если и только если  правильная. Если  неквадратная, ситуация несколько усложняется. Пусть  - наименьший общий знаменатель всех элементов  и . Умножение (6.4) на  приводит к

                                                           (6.5)

где  и  q*p и q*r полиномиальные матрицы. Если  и, следовательно,  полного строчного ранга, то существует такая унимодальная полиномиальная матрица , что  строчно приведенная.