Полюса и нули. Полюса и передаточные нули. Передаточные нули и блокирование сигнала. Вычисление передаточных нулей. Блокирующие нули, страница 2

                                (3.8)

что ввиду (3.7) тождественно равно нулю для любых k . Это свойство, а именно, что  для t ≥ 0 существует, если и только если - передаточный нуль G(s). Следовательно, это может быть использовано для характеризации передаточных нулей G(s) для случая q < p . Таким образом, получили свойства, которые сформулируем в виде следствия.

Следствие 3.2. ( Передаточно - блокирующие свойство- transmission – blocking property). Рассмотрим многоканальную систему с q*p правильной рациональной матрицей G(s) . Предполагается, что G(s)  имеет полный ранг, Взаимно простое разложение  и несократимую реализацию  Тогда:

1. Если q ≥ p и если  передаточный нуль G(s), тогда существует ненулевой p*1 числовой вектор из постоянных k такой, что выход системы, соответствующий начальному состоянию  и входу  тождественно равен нулю.

2. Если q < p если  передаточный нуль, но не полюс G(s), тогда для входа , где k произвольный p*1 числовой вектор f такой, что выход, соответствующий  и начальному состоянию  имеет свойство

Ввиду этого передаточно – блокирующего свойства, нули, описанные в определении 3.3, называют передаточными нулями.

3.3 Вычисление передаточных нулей

Передаточные нули могут быть определены с использованием динамических уравнений. Рассмотрим систему с взаимно простым разложением  и неприводимым динамическим уравнением  Рассмотрим системную матрицу

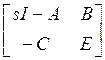≜                                (3.9)

Если матрицы  A, B, C, и E имеют ранг n*n, n*p, q*n и q*p соответственно, тогда матрица  имеет размеры (n+q)*(n+p). Хотя элементы  полиномы, мы будем их рассматривать как элементы поля рациональных функций. Ввиду

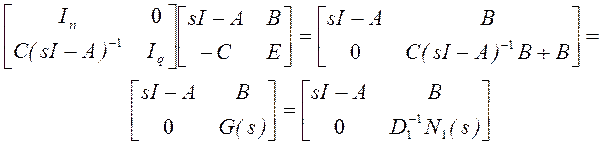
мы имеем

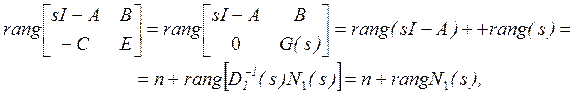               (3.10)

где ранг подразумевается над полем рациональных функций. Если G(s) имеет полный ранг, т.е. , тогда

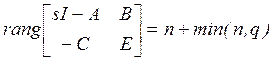                                               .                          (3.11)

Если заменить s на элементы из ℂ, то S(s) становится матрицей над ℂ полного ранга. Практически доказали следующую теорему.

Теорема 3.5. Рассмотрим q*p правильную рациональную матрицу G(s) полного ранга и неприводимым представлением  Если  не полюс G(s), тогда передаточный нуль G(s), если и только если

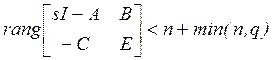                        (3.12)

В дальнейшем ограничение на  не быть полюсом G(s) может быть опущено.

Теорема 3.6. Рассмотрим q*p правильную рациональную матрицу G(s) полного ранга и с n- мерным неприводимой реализацией  Тогда  будет передаточным нулем, G(s) если и только если

.

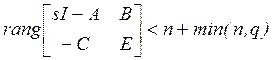Доказательство. Пусть . Представим G(s) как

                 (3.13) где  строго правильное и взаимно простое разложение слева и D(s) строчно приведенная матрица. Перейдем к неприводимому такому, что

                ;                                (3.14)

                                                                      (3.15)

где  определено как в (3.16):

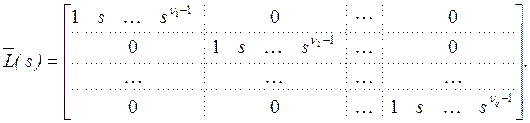                 (3.16)

Таким образом, имеем  взаимно простые слева и  взаимно простые справа, следовательно, из теорем 2.8 и 2.9 следует существование матриц , таких, что

;

, которые вместе с  могут быть записаны в матричной форме

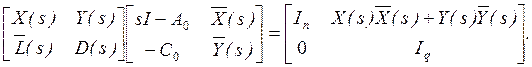                (3.17)