Полюса и нули. Полюса и передаточные нули. Передаточные нули и блокирование сигнала. Вычисление передаточных нулей. Блокирующие нули, страница 3

Очевидно, что матрица справа унимодальная, следовательно, слева матрицы унимодальные.

Вычислим

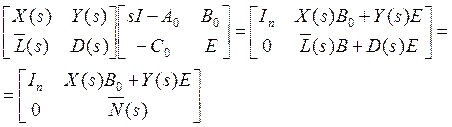                         (3.18)

На последнем шаге мы использовали , что следует из (3.13) и (3.15). Так как самая левая матрица в (3.18) унимодальная, что для каждого s в ℂ.

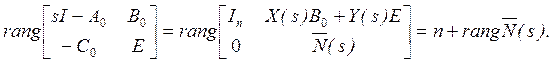
Ввиду того, что  и  обе взаимно простые реализации G(s), они строго системно эквивалентны. Отсюда мы имеем, что для каждого s

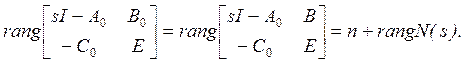                (3.19)

и теорема следует из определения передаточного нуля.

3.4   Блокирующие нули

Идея передаточных нулей, веденная выше, это одна из многих возможных путей определения нулей для рациональных матриц. Далее мы введем еще одно из возможных определений.

Определение 3.4. Рассмотрим q*p правильную рациональную матрицу G(s). Пусть  наибольший общий делитель числителей всех элементов G(s). Тогда корни  называют блокирующими нулями ( blocking zeros) матрицы G(s).

Пример 3.3. Рассмотрим

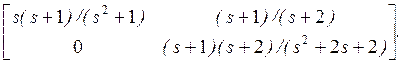
Наибольший общий делитель трех числителей G(s) равен s+1. Следовательно, -1 единственный блокирующий ноль G(s). Можно показать, что передаточные нули G(s) 0, -1, и –2.

Из примера видим, что определения передаточных и блокирующих нулей не эквивалентны. Если каждый элемент G(s) неприводим, блокирующие нули никогда не могут быть полюсами G(s) . с другой стороны, передаточные нули могут быть полюсами G(s) . если имеем дело со скалярными передаточными  функциями, то нет различия между передаточными и блокирующими нулями.

Аналогично передаточным нулям, блокирующие нули обладают свойством «блокирования» некоторых мод при прохождении через устройство. Пусть u_i(s) i=   i-я компонента входного вектора u(s) и

U_i(s)=f_i(s)/φ(s), i=(3.20)

где  и f_i(s) полиномы. Пусть s=a– корень . Если e^at появляется в выходном сигнале y_i(t), то говорят, что s-a появляется как мода y_i(t).

Теорема 3.7. Рассмотрим систему с правильной передаточной матрицей G(s). Пусть вход u(s) имеет вид (3.20). Тогда для любых начальных состояний нет корней , которые  появились бы как моды входного сигнала, если и только если каждый  корень является блокирующим нулём G(s).

Доказательство. Если каждый корень является блокирующим нулём G(s), то G(s) не включает корней , соответствующих полюсам. Следовательно, для любых начальных состояний, реакция системы при нулевом входе не включает каких либо мод, соответствующих корням . Пусть y_i(s) будет i-й компонентой выходного вектора y(s) и пусть G(s)=[g_ij(s)]. Тогда реакция системы при нулевом начальном состоянии определяется

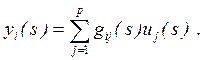                                  (3.21)

Пусть β(s) – наибольший общий делитель всех числителей g_ij(s). Тогда мы можем записать g_ij(s) так

и преобразовать (3.21), используя (3.20):

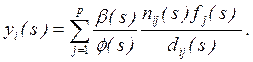
Если каждый корень  есть блокирующий нуль, то  делит β(s). Следовательно, ни один корень  не появится как мода y_i(t).

Сейчас предположим, что корень s-a полинома не есть блокирующий нуль. Тогда существует по крайней мере один n_kl(s), не содержащий s-a в качестве множителя: другими словами, s-a будет блокирующим нулём. Выберем f_i(s)=0 для  и , тогда

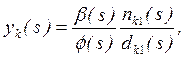
s-a появится в качестве моды y_k(t). Это завершает доказательство теоремы.