Достижимость, минимальность, развязанные нули. Выходной развязанный нуль, ненаблюдаемость, хорошая сформированность, степень Макмиллана, биправильность, индекс управляемости, распределения, экспоненциальная устойчивость, правое/левое взаимно простое разложение, внутренняя правильность

4.  ДОСТИЖИМОСТЬ, МИНИМАЛЬНОСТЬ, РАЗВЯЗАННЫЕ НУЛИ

Выходной развязанный нуль, ненаблюдаемость, хорошая сформированность, степень Макмиллана, биправильность, индекс управляемости, распределения, экспоненциальная устойчивость, правое/левое взаимно простое разложение, внутренняя правильность.

Вводятся понятия достижимости, наблюдаемости, степени Макмиллана, правого-левого и левого-правого разложения матричных передаточных функций. Многомерные системы существенно “богаче” одномерных: имеется несколько типов нулей, например входные и выходные нули. Существует связь между минимальностью и наличием развязанных нулей, Читатель знакомится с такими понятиями, как хорошая сформированность (устроенность), приведенность. Для матричного описания прослеживается понятие индексов управляемости. Следует уделить внимание пунктам S68, S71, S73, S81, $25. При первом чтении доказательство в S65 можно пропустить.

S63.  Введем несколько простейших понятий, связанных с траекториями решений. Пусть система описывается матричными полиномиальными уравнениями

                         D(p)x(t) = N_l(p)u(t),  y(t) = N_r(p)x(t) + K(p)u(t).                               (а)

Здесь x - псевдосостояние,  – порядок полиномиального описания . Его называют характеристическим полиномом полиномиального матричного описания (characteristic polynomial of the polynomial matrix system description or PMD), а собственные значения этого полинома – собственными значениями полиномиального матричного описания (eigenvalue of PMD). При  псевдосостояние x вычисляется через вектор состояния  и фундаментальную матрицу  либо через вектор : , где Р – невырожденная числовая матрица. Решение  при  называют траекторией псевдосостояния при нулевом выходе (zero-input pseudo-state trajectory), и оно равно . Выход объекта y(t) при  называют реакцией на нулевой вход (zero-input response). Решение  для  при нулевых начальных условиях

                                                                                              (б)

называют траекторией псевдосостояния полиномиального матричного описания при нулевых начальных условиях (zero-state pseudo-state trajectory of the PMD). Здесь

,

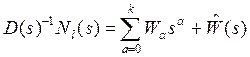где  - числовая матрица,  - строго правильная передаточная функция. В оригиналах уравнение (б) – это обычная свертка:

.

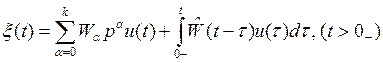Передаточная функция для (а):

При ненулевых начальных условиях вектор псевдосостояния

.

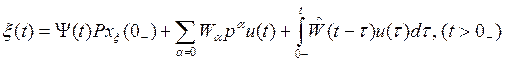S64.  Траектория псевдосостояния x(t) системы (S63,а) при нулевом входе называется достижимой (reachable), если , которое производит траекторию x₁(×) такую, что x₁(t) = x(t) для t > 0. Другими словами,  такое, что вектор  состоит из двух частей: x₁(s) = x(s) + h(s). Здесь  - полиномиальная часть , и для нее справедливо  для .

S65.  Даны  и  такие, что  , где L – наибольший общий делитель. Тогда траектория x(×) псевдосостояния при нулевом входе для D = [D, N_l, N_r, K] достижима тогда и только тогда, когда  при "t ³ 0.

Д о к а з а т е л ь с т в о. Пусть траектория псевдосостояния при нулевом входе x(t) достижима, что соответствует  при . Покажем, что  при . Перейдем к изображениям

                                             .                                                (а)

Здесь p(s) – полиномиальный вектор, соответствующий начальным условиям. Из S64 следует, что существует управление  (это равносильно ) такое, что

                                                                                               (б)

где

                                      .                                          (в)

Начальных условий, а они определяются p(s), меньше по сравнению с порядком уравнения. Порядок уравнения определяется D(s). Поэтому . Подставим (в) в (б):

и вспомним (а):

откуда

Здесь мы использовали условие  . Выражение в квадратных скобках обозначим через :

                                                                                   (г)

Несложно увидеть, что это полиномиальный вектор. Итак, получили

                                                                                                          (д)

Полиномиальный вектор начальных условий p(s) делится слева без остатка на . Подставим (д) в (а):

откуда

                                                                                     (е)

Последнее включение получено из того, что начальных условий меньше порядка уравнений. Формула (е) может быть прочитана так: реакция x(t) системы  начинается из нуля и возникает из-за действия входа . Так как  - полиномиальный вектор, его можно записать так: , что в оригиналах соответствует  Здесь d(t) – функция Дирака (Dirac function). Используем последнее соотношение в (е) при переходе к оригиналам:

.

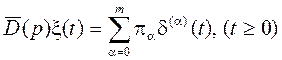Имеем ввиду, что для  при всех , откуда

                                                                                                             (ж)

при , т.е. x(t) – это решение дифференциального уравнения (ж). Надо учесть, что x(0) в (ж) уже не нуль, поэтому (ж) справедливо при .